Thi thử tốt nghiệp THPT quốc gia môn Toán online - Đề thi của trường THPT Trần Quý Cáp năm 2022

Thí sinh đọc kỹ đề trước khi làm bài.

Tổng số câu hỏi: 0

Câu 1:

Cho tứ diện $ABCD$, trên các cạnh $BC,\,\,BD,\,\,AC$ lần lượt lấy các điểm $M,\,\,N,\,\,P$ sao cho $BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP$. Mặt phẳng $\left( {MNP} \right)$ chia khối tứ diện $ABCD$ thành 2 phần có thể tích là ${V_1},\,\,{V_2}$. Tính tỉ số $\dfrac{{{V_1}}}{{{V_2}}}$

A. $\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{26}}{{19}}$

B. $\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{3}{{19}}$

C. $\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{15}}{{19}}$

D. $\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{26}}{{13}}$

Câu 2:

Có bao nhiêu giá trị nguyên của tham số $m \in \left[ { - 10;10} \right]$ để bất phương trình sau nghiệm đúng $\forall x \in \mathbb{R}$: ${\left( {6 + 2\sqrt 7 } \right)^x} + \left( {2 - m} \right){\left( {3 - \sqrt 7 } \right)^x} - \left( {m + 1} \right){2^x} \ge 0$?

A. 10

B. 9

C. 12

D. 11

Câu 3:

Cho lăng trụ đứng $ABC.A'B'C'$ có diện tích tam giác $ABC$ bằng $2\sqrt 3 $. Gọi $M,\,\,N,\,\,P$ lần lượt thuộc các cạnh $AA',\,\,BB',\,\,CC'$, diện tích tam giác $MNP$ bằng 4. Tính góc giữa hai mặt phẳng $\left( {ABC} \right)$ và $\left( {MNP} \right)$.

A. ${120^0}$

B. ${45^0}$

C. ${30^0}$

D. ${90^0}$

Câu 4:

Cho hàm số $f\left( x \right),\,\,f\left( { - x} \right)$ liên tục trên $\mathbb{R}$ và thỏa mãn $2f\left( x \right) + 3f\left( { - x} \right) = \dfrac{1}{{4 + {x^2}}}$. Tính $I = \int\limits_{ - 2}^2 {f\left( x \right)dx} $.

A. $I = \dfrac{\pi }{{20}}$

B. $I = \dfrac{\pi }{{10}}$

C. $I = - \dfrac{\pi }{{20}}$

D. $I = - \dfrac{\pi }{{10}}$

Câu 5:

Cho $\int\limits_1^2 {f\left( x \right)dx} = 2$. Tính $\int\limits_1^4 {\dfrac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}dx} $ bằng :

A. $I = 4$

B. $I = 1$

C. $I = \dfrac{1}{2}$

D. $I = 2$

Câu 6:

Cho các số thực dương $a,\,\,b$ với $a \ne 1$ và ${\log _a}b > 0$. Khẳng định nào sau đây là đúng ?

A. $\left[ \begin{array}{l}0 < a,\,\,b < 1\\0 < a < 1 < b\end{array} \right.$

B. $\left[ \begin{array}{l}0 < a,\,\,b < 1\\1 < a,\,\,b\end{array} \right.$

C. $\left[ \begin{array}{l}0 < a,\,\,b < 1\\0 < b < 1 < a\end{array} \right.$

D. $\left[ \begin{array}{l}0 < b < 1 < a\\1 < a,\,\,b\end{array} \right.$

Câu 7:

Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = {x^2}\left( {x - 1} \right){\left( {{x^2} - 1} \right)^3},\,\,\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là:

A. 2

B. 1

C. 8

D. 3

Câu 8:

Cho hai tích phân $\int\limits_{ - 2}^5 {f\left( x \right)dx} = 8$ và $\int\limits_5^{ - 2} {g\left( x \right)dx} = 3$. Tính $I = \int\limits_{ - 2}^5 {\left[ {f\left( x \right) - 4g\left( x \right) - 1} \right]dx} $ ?

A. $I = 13$

B. $I = 27$

C. $I = - 11$

D. $I = 3$

Câu 9:

Cho hình chóp đều $S.ABCD$ có đáy là hình vuông $ABCD$ tâm $O$ cạnh $2a$, cạnh bên $SA = a\sqrt 5 $. Khoảng cách giữa $BD$ và $SC$ là :

A. $\dfrac{{a\sqrt {15} }}{5}$

B. $\dfrac{{a\sqrt {30} }}{5}$

C. $\dfrac{{a\sqrt {15} }}{6}$

D. $\dfrac{{a\sqrt {30} }}{6}$

Câu 10:

Rút gọn biểu thức $P = \frac{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}{{{a^{4 - \sqrt 5 }}.{a^{\sqrt 5 - 2}}}}$ (với $a > 0$ và $a \ne 1$ )

A. $P = 1$

B. $P = a$

C. $P = 2$

D. $P = {a^2}$

Câu 11:

Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số $m$ để phương trình $f\left( {\cos x} \right) = m$ có 2 nghiệm phân biệt thuộc $\left( {0;\dfrac{{3\pi }}{2}} \right]$ là:

A. $\left[ { - 2;2} \right]$

B. $\left( {0;2} \right)$

C. $\left( { - 2;2} \right)$

D. $\left[ {0;2} \right)$

Câu 12:

Cho hàm số $y = f\left( x \right)$ bảng biến thiên như sau:

Phát biểu nào sau đây đúng?

A. Hàm số đạt cực đại tại $x = 2$

B. Hàm số đạt cực đại tại $x = 4$

C. Hàm số có 3 cực tiểu

D. Hàm số có giá trị cực tiểu là 0

Câu 13:

Trong không gian với hệ tọa độ $Oxyz$ cho ba điểm $A\left( {1;0;0} \right);\,\,B\left( {0;2;0} \right);\,\,C\left( {0;0;3} \right)$. Thể tích tứ diện $OABC$ bằng:

A. $\dfrac{1}{3}$

B. $\dfrac{1}{6}$

C. $1$

D. $2$

Câu 14:

Gọi $m$ và $M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = x - \sqrt {4 - {x^2}} $. Khi đó $M - m$ bằng:

A. $4$

B. $2\left( {\sqrt 2 - 1} \right)$

C. $2 - \sqrt 2 $

D. $2\left( {\sqrt 2 + 1} \right)$

Câu 15:

Cho mặt phẳng $\left( P \right)$ đi qua các điểm $A\left( { - 2;0;0} \right);\,\,B\left( {0;3;0} \right);\,\,C\left( {0;0; - 3} \right)$. Mặt phẳng $\left( P \right)$ vuông góc với mặt phẳng nào trong các mặt phẳng sau:

A. $3x - 2y + 2z + 6 = 0$

B. $2x + 2y - z - 1 = 0$

C. $x + y + z + 1 = 0$

D. $x - 2y - z - 3 = 0$

Câu 16:

Trong không gian với hệ tọa độ $Oxyz$ cho bốn điểm $A\left( {1;0;2} \right),\,\,\,B\left( { - 2;1;3} \right),\,\,C\left( {3;2;4} \right),$ $D\left( {6;9; - 5} \right)$. Tọa độ trọng tâm của tứ diện $ABCD$ là:

A. $\left( {2;3;1} \right)$

B. $\left( {2;3; - 1} \right)$

C. $\left( { - 2;3;1} \right)$

D. $\left( {2; - 3;1} \right)$

Câu 17:

Tập xác định của hàm số ${\left( {{x^2} - 3x + 2} \right)^\pi }$ là:

A. $\mathbb{R}\backslash \left\{ {1;2} \right\}$

B. $\left( {1;2} \right)$

C. $\left( { - \infty ;1} \right] \cup \left[ {2; + \infty } \right)$

D. $\left( { - \infty ;1} \right) \cup \left( {2; + \infty } \right)$

Câu 18:

Trong không gian $Oxyz$, cho mặt cầu có phương trình ${x^2} + {y^2} + {z^2} - 2x + 4y - 6z + 9 = 0$. Tọa độ tâm $I$ và bán kính $R$ của mặt cầu là:

A. $I\left( {1; - 2;3} \right)$ và $R = 5$

B. $I\left( { - 1;2; - 3} \right)$ và $R = 5$

C. $I\left( {1; - 2;3} \right)$ và $R = \sqrt 5 $

D. $I\left( { - 1;2; - 3} \right)$ và $R = \sqrt 5 $

Câu 19:

Tích phân $\int\limits_0^2 {\dfrac{x}{{{x^2} + 3}}dx} $ bằng:

A. $\dfrac{1}{2}\log \dfrac{7}{3}$

B. $\ln \dfrac{7}{3}$

C. $\dfrac{1}{2}\ln \dfrac{3}{7}$

D. $\dfrac{1}{2}\ln \dfrac{7}{3}$

Câu 20:

Tìm mệnh đề sai trong các mênh đề sau:

A. $\int\limits_{}^{} {2{e^x}dx} = 2\left( {{e^x} + C} \right)$

B. $\int\limits_{}^{} {{x^3}dx} = \dfrac{{{x^4} + C}}{4}$

C. $\int\limits_{}^{} {\dfrac{1}{x}dx} = \ln x + C$

D. $\int\limits_{}^{} {\sin xdx} = - \cos x + C$

Câu 21:

Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ vàc cos bảng biến thiên như sau:

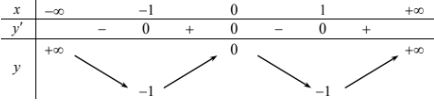
Tìm tất cả các giá trị thực của tham số m để phương trình $f\left( x \right) - 1 = m$ có đúng 2 nghiệm.

A. $ - 2 < m < - 1$

B. $m > 0,\,\,m = - 1$

C. $m = - 2,\,\,m > - 1$

D. $m = - 2,\,\,m \ge - 1$

Câu 22:

Trong không gian với hệ trục tọa độ $Oxyz$, cho $\overrightarrow a = - \overrightarrow i + 2\overrightarrow j - 3\overrightarrow k $. Tọa độ của vectơ $\overrightarrow a $ là:

A. $\left( { - 3;2; - 1} \right)$

B. $\left( {2; - 1; - 3} \right)$

C. $\left( { - 1;2; - 3} \right)$

D. $\left( {2; - 3; - 1} \right)$

Câu 23:

Cho hàm số $f\left( x \right)$ có $f\left( 2 \right) = f\left( { - 2} \right) = 0$ và có bảng xét dấu của đạo hàm như sau:

Hàm số $y = {\left( {f\left( {3 - x} \right)} \right)^2}$ nghịch biến trên khoảng nào dưới đây?

A. $\left( {2;5} \right)$

B. $\left( {1; + \infty } \right)$

C. $\left( { - 2; - 1} \right)$

D. $\left( {1;2} \right)$

Câu 24:

Tính khoảng cách giữa các tiếp tuyến của đồ thị hàm $f\left( x \right) = {x^3} - 3x + 1\,\,\left( C \right)$ tại cực trị của $\left( C \right)$.

A. 4

B. 1

C. 2

D. 3

Câu 25:

Khối trụ tròn xoay có đường kính là $2a$, chiều cao là $h = 2a$ có thể tích là:

A. $V = 2\pi {a^2}$

B. $V = 2\pi {a^3}$

C. $V = 2\pi {a^2}h$

D. $V = \pi {a^3}$

Câu 26:

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

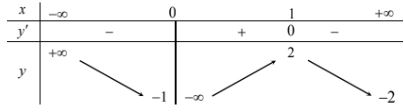
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:

A. 3

B. 4

C. 1

D. 2

Câu 27:

Gọi $l,\,\,h,\,\,r$ lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diệnt ích xung quanh ${S_{xq}}$ của hình nón là:

A. ${S_{xq}} = \dfrac{1}{3}\pi {r^2}h$

B. ${S_{xq}} = \pi rh$

C. ${S_{xq}} = 2\pi rl$

D. ${S_{xq}} = \pi rl$

Câu 28:

Cho hàm số $y = f\left( x \right)$ có $f'\left( x \right)$ liên tục trên $\left[ {0;2} \right]$ và $f\left( 2 \right) = 16$; $\int\limits_0^2 {f\left( x \right)dx} = 4$. Tính $I = \int\limits_0^1 {xf'\left( {2x} \right)dx} $

A. $I = 7$

B. $I = 20$

C. $I = 12$

D. $I = 13$

Câu 29:

Cho khối hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = a,\,\,AD = b,\,AA' = c$. Thể tích khối hộp chữ nhật $ABCD.A'B'C'D'$ bằng bao nhiêu?

A. $\dfrac{1}{3}abc$

B. $3abc$

C. $abc$

D. $\dfrac{1}{2}abc$

Câu 30:

Đặt $a = {\log _2}5,\,\,b = {\log _3}5$. Hãy biểu diễn ${\log _6}5$ theo $a$ và $b$.

A. ${\log _6}5 = \dfrac{1}{{a + b}}$

B. ${\log _6}5 = \dfrac{{ab}}{{a + b}}$

C. ${\log _6}5 = {a^2} + {b^2}$

D. ${\log _6}5 = a + b$

Câu 31:

Cho hàm số $y = f\left( x \right),\,\,y = g\left( x \right)$ liên tục trên $\left[ {a;b} \right]$ và số thực $k$ tùy ý. Trong các khẳng định sau, khẳng định nào sai?

A. $\int\limits_a^a {kf\left( x \right)dx} = 0$

B. $\int\limits_a^b {xf\left( x \right)dx} = x\int\limits_a^b {f\left( x \right)dx} $

C. $\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} $

D. $\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} $.

Câu 32:

Chọn ngẫu nhiên một số tự nhiên gồm 7 chữ số khác nhau có dạng $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}} $. Tính xác suấ để số được chọn luôn có mặt chữ số 2 và thỏa mãn ${a_1} < {a_2} < {a_3} < {a_4} > {a_5} > {a_6} > {a_7}$.

A. $\dfrac{1}{{243}}$

B. $\dfrac{1}{{486}}$

C. $\dfrac{1}{{1215}}$

D. $\dfrac{1}{{972}}$

Câu 33:

Cho $f\left( x \right)$ là hàm số chẵn, liên tục trên đoạn $\left[ { - 1;1} \right]$ và $\int\limits_{ - 1}^1 {f\left( x \right)dx} = 4$. Kết quả $I = \int\limits_{ - 1}^1 {\dfrac{{f\left( x \right)}}{{1 + {e^x}}}dx} $ bằng:

A. $I = 8$

B. $I = 4$

C. $I = 2$

D. $I = \dfrac{1}{4}$

Câu 34:

Cho khối lăng trụ $ABC.A'B'C'$ có thể tích bằng $V$. Tính thể tích khối tứ diện $ABCB'C'$.

A. $\dfrac{V}{4}$

B. $\dfrac{V}{2}$

C. $\dfrac{{3V}}{4}$

D. $\dfrac{{2V}}{3}$

Câu 35:

Một khối gỗ hình lập phương có thể tích ${V_1}$. Một người thợ mộc muốn gọt giũa khối gỗ đó thành một khối trụ có thể tích là ${V_2}$. Tính tỉ số lớn nhất $k = \dfrac{{{V_2}}}{{{V_1}}}$?

A. $k = \dfrac{\pi }{4}$

B. $k = \dfrac{2}{\pi }$

C. $k = \dfrac{\pi }{2}$

D. $k = \dfrac{4}{\pi }$

Câu 36:

Cho hàm số $y = f\left( x \right)$ có bảng biế thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $\left( { - \infty ; - 1} \right)$

B. $\left( { - 1;1} \right)$

C. $\left( {1; + \infty } \right)$

D. $\left( {0;1} \right)$

Câu 37:

Tính $\lim \dfrac{{\sqrt {4{n^2} + 1} - \sqrt {n + 2} }}{{2n - 3}}$ bằng:

A. $ + \infty $

B. $1$

C. $2$

D. $\dfrac{3}{2}$

Câu 38:

Tìm tập nghiệm của bất phương trình ${\log _{\frac{2}{5}}}\left( {x - 4} \right) + 1 > 0$.

A. $\left[ {\dfrac{{13}}{2}; + \infty } \right)$

B. $\left( { - \infty ;\dfrac{{13}}{2}} \right)$

C. $\left( {4; + \infty } \right)$

D. $\left( {4;\dfrac{{13}}{2}} \right)$

Câu 39:

Có bao nhiêu số tự nhiên có bốn chữ số khác nhau được tạo thành từ các chữ số của tập $X = \left\{ {1;3;5;8;9} \right\}$.

A. ${P_5}$

B. ${P_4}$

C. $C_5^4$

D. $A_5^4$

Câu 40:

Cho cấp số nhân $\left( {{u_n}} \right)$ có tổng $n$ số hạng đầu tiên là ${S_n} = {6^n} - 1$. Tìm số hạng thứ năm của cấp số cộng đã cho

A. $6480$

B. $6840$

C. $7775$

D. $120005$

Câu 41:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A\left( {0; - 2; - 1} \right);\,\,B\left( { - 2; - 4;3} \right);\,\,C\left( {1;3; - 1} \right)$. Tìm điểm $M \in \left( {Oxy} \right)$ sao cho $\left| {\overrightarrow {MA} + \overrightarrow {MB} + 3\overrightarrow {MC} } \right|$ đạt giá trị nhỏ nhất.

A. $\left( {\dfrac{1}{5};\dfrac{3}{5};0} \right)$

B. $\left( { - \dfrac{1}{5};\dfrac{3}{5};0} \right)$

C. $\left( {\dfrac{1}{5}; - \dfrac{3}{5};0} \right)$

D. $\left( {\dfrac{3}{4};\dfrac{4}{5};0} \right)$

Câu 42:

Tìm tất cả các giá trị thực của m để hàm số $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} - 4mx$ đồng biến trên đoạn $\left[ {1;4} \right]$.

A. $m \in \mathbb{R}$

B. $m \le \dfrac{1}{2}$

C. $\dfrac{1}{2} < m < 2$

D. $m \le 2$

Câu 43:

Trong không gian với hệ tọa độ Oxyz, cho các vectơ $\overrightarrow a = \left( {2;m - 1;3} \right);\,\,\overrightarrow b = \left( {1;3; - 2n} \right)$. Tìm $m,n$ để các vectơ $\overrightarrow a ,\,\,\overrightarrow b $ cùng hướng.

A. $m = 7,\,\,n = \dfrac{{ - 3}}{4}$

B. $m = 1,\,\,n = 0$

C. $m = 7,\,\,n = \dfrac{{ - 4}}{3}$

D. $m = 4,\,\,n = - 3$

Câu 44:

Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực $\mathbb{R}$?

A. $y = {\left( {\dfrac{2}{e}} \right)^x}$

B. $y = {\left( {\dfrac{\pi }{3}} \right)^x}$

C. $y = {\log _{\dfrac{\pi }{4}}}\left( {2{x^2} + 1} \right)$

D. $y = {\log _{\dfrac{1}{2}}}x$

Câu 45:

Mệnh đề nào sau đây Sai?

A. $\forall \,x \in \mathbb{R},\,{e^x} > 0$

B. $\forall \,x \in \,\mathbb{R},\,{e^{{x^2}}} \ge 1$

C. $\forall \,x \in \mathbb{R},\,{e^{ - x}} < 1$

D. $\forall \,x \in \mathbb{R},\,\frac{1}{e} \le {e^{\sin \,x}} \le e$

Câu 46:

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = x,\,AD = 1.$ Biết rằng góc giữa đường thẳng $A'C$ và mặt phẳng $\left( {ABB'A'} \right)$ bằng ${30^0}.$ Tìm giá trị lớn nhất ${V_{\max }}$ của thể tích khối hộp $ABCD.A'B'C'D'$

A. ${V_{\max }} = \frac{{\sqrt 3 }}{4}$

B. ${V_{\max }} = \frac{1}{2}$

C. ${V_{\max }} = \frac{3}{2}$

D. ${V_{\max }} = \frac{{3\sqrt 3 }}{4}$

Câu 47:

Cho biết ${\left( {x - 2} \right)^{\frac{{ - 1}}{3}}} > {\left( {x - 2} \right)^{\frac{{ - 1}}{6}}},$ khẳng định nào sau đây Đúng?

A. $2 < x < 3$

B. $0 < x < 1$

C. $x > 2$

D. $x > 1$

Câu 48:

Trong tất cả các hình thang cân có cạnh bên bằng $2$ và cạnh đáy nhỏ bằng $4$ , tính chu vi $P$ của hình thang có diện tích lớn nhất.

A. $P = 12$

B. $P = 8$

C. $P = 10 + 2\sqrt 3 $

D. $5 + \sqrt 3 $

Câu 49:

Cho ${\log _8}\left| x \right| + {\log _4}{y^2} = 5$ và ${\log _8}\left| y \right| + {\log _4}{x^2} = 7.$ Tìm giá trị của biểu thức $P = \left| x \right| - \left| y \right|.$

A. $P = 64$

B. $P = 56$

C. $P = 16$

D. $P = 8$

Câu 50:

Trải mặt xung quanh của một hình nón lên một mặt phẳng ta được hình quạt (xem hình bên dưới) là phần của hình tròn có bán kính bằng $3cm.$ Bán kính đáy $r$ của hình nón ban đầu gần nhất với số nào dưới đây?

A. $2,25$

B. $2,26$

C. $2,23$

D. $2,24$