Thi thử THPT quốc gia môn Toán online - Đề thi của Trường THPT Nguyễn Kiệm năm 2023

Thí sinh đọc kỹ đề trước khi làm bài.

Tổng số câu hỏi: 0

Câu 1:

Cho $f\left( 1 \right)=2$ và $\int\limits_{1}^{3}{{f}'\left( x \right)dx}=6$ tính $f\left( 3 \right)$

A. $f\left( 3 \right)=8.$

B. $f\left( 3 \right)=-4$.

C. $f\left( 3 \right)=4$.

D. $f\left( 3 \right)=3$.

Câu 2:

Nghiệm của phương trình ${{2}^{2x-1}}=8$ là

A. $x=\frac{3}{2}.$

B. $x=\frac{5}{2}.$

C. $x=3.$

D. $x=2.$

Câu 3:

Tiệm cận đứng của đồ thị hàm số $y=\frac{2x-1}{x+1}$ là đường thẳng có phương trình

A. $y=-1.$

B. $y=2.$

C. $x=-1.$

D. $x=2.$

Câu 4:

Trong hình vẽ dưới đây, điểm $M$ là điểm biểu diễn của số phức nào?

A. $1-2i.$

B. $2+i.$

C. $1+2i.$

D. $2-i.$

Câu 5:

Trong không gian $Oxyz$, phương trình nào dưới đây là phương trình của mặt cầu tâm $I\left( 1;\ 0;\ -2 \right),$ bán kính $R=4?$

A. ${{\left( x+1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=16.$

B. ${{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z+2 \right)}^{2}}=16.$

C. ${{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z+2 \right)}^{2}}=4.$

D. ${{\left( x+1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=4.$

Câu 6:

Tập xác định của hàm số $y=\ln \left( 2-x \right)$ là

A. $D=\left( -\infty ;2 \right).$

B. $D=\mathbb{R}\backslash \left\{ 2 \right\}.$

C. $D=\left( 2;+\infty \right).$

D. $D=\mathbb{R}.$

Câu 7:

Cho hình hộp đứng có đáy là hình vuông cạnh bằng $a,$ độ dài cạnh bên bằng $3a.$ Thể tích của khối hộp đã cho bằng

A. $9{{a}^{3}}.$

B. ${{a}^{3}}.$

C. $3{{a}^{3}}.$

D. $\frac{1}{3}{{a}^{3}}.$

Câu 8:

Một nguyên hàm của hàm số $f\left( x \right)=\sin \left( 2x-\frac{\pi }{3} \right)$ là

A. $F\left( x \right)=\frac{1}{2}\cos \left( 2x-\frac{\pi }{3} \right).$

B. $F\left( x \right)=\cos \left( 2x-\frac{\pi }{3} \right).$

C. $F\left( x \right)=-\frac{1}{2}\cos \left( 2x-\frac{\pi }{3} \right).$

D. $F\left( x \right)=-\cos \left( 2x-\frac{\pi }{3} \right).$

Câu 9:

Một cấp số nhân gồm ba số hạng, biết số hạng thứ nhất và thứ hai lần lượt là $-1;\,3.$ Số hạng cuối của cấp số nhân đó bằng

A. $7.$

B. $9.$

C. $-9.$

D. $-12.$

Câu 10:

Trong không gian $Oxyz,$ mặt phẳng $\left( \alpha \right):-2x+3y-z+5=0$ đi qua điểm nào dưới đây?

A. $N\left( 5;\ 1;\ -2 \right).$

B. $Q\left( 2;\ 1;\ -1 \right).$

C. $M\left( 2;\ 2;\ -3 \right).$

D. $P\left( -3;\ 2;\ 4 \right).$

Câu 11:

Cho mặt cầu có đường kính bằng $8.$ Diện tích của mặt cầu đã cho bằng

A. $256\pi .$

B. $\frac{256\pi }{3}.$

C. $64\pi .$

D. $\frac{64\pi }{3}.$

Câu 12:

Biết ${\int\limits_{0}^{1}{f\left( x \right)\text{d}x=-2}}$ và ${\int\limits_{0}^{5}{f\left( x \right)\text{d}x=3},}$ khi đó ${\int\limits_{1}^{5}{2f\left( x \right)\text{d}x}}$ bằng

A. $10.$

B. $5.$

C. $2.$

D. $1.$

Câu 13:

Cho hai số phức ${{z}_{1}}=1-2i$ và ${{z}_{2}}=3+4i.$ Số phức ${{z}_{1}}.{{z}_{2}}$ bằng

A. $-2+11i.$

B. $-2-11i.$

C. $11+2i.$

D. $11-2i.$

Câu 14:

Đồ thị hàm số $y=\frac{x-4}{2x+2}$ cắt trục tung tại điểm có tung độ bằng

A. $-2.$

B. $\frac{1}{2}.$

C. $4.$

D. $-1.$

Câu 15:

Trong không gian $Oxyz,$ đường thẳng $d:\left\{ \begin{align} & x=1-t \\ & y=2+2t \\ & z=3-t \\\end{align} \right.$ có một vectơ chỉ phương là

A. $\overrightarrow{{{u}_{3}}}=\left( 1\,;\ -2\,;\ -1 \right).$

B. $\overrightarrow{{{u}_{4}}}=\left( 1\,;\ 2\,;\ 3 \right).$

C. $\overrightarrow{{{u}_{1}}}=\left( 1\,;\ 2\,;\ 1 \right).$

D. $\overrightarrow{{{u}_{2}}}=\left( 1\,;\ -2\,;\ 1 \right).$

Câu 16:

Đạo hàm của hàm số $y={{5}^{2x}}$ là

A. ${y}'={{5}^{2x}}\ln 25.$

B. ${y}'=\frac{{{5}^{2x}}}{\ln 5}.$

C. ${y}'={{5}^{2x}}\ln 5.$

D. ${y}'=\frac{{{5}^{2x}}}{\ln 25}.$

Câu 17:

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ:

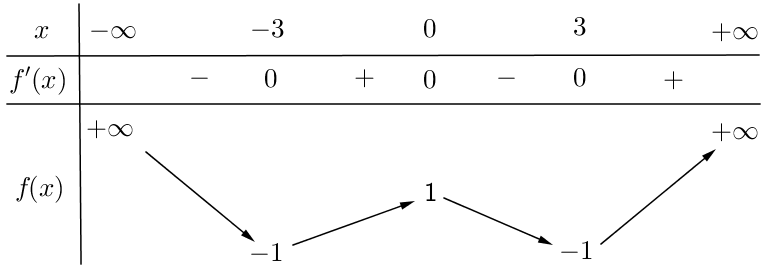
Số điểm cực trị của hàm số đã cho bằng

A. $2$.

B. $3$.

C. $0$.

D. $1$.

Câu 18:

Tập nghiệm của bất phương trình ${{\log }_{3}}\left( x-2 \right)\le 2$ là

A. $S=\left( 2;11 \right]$.

B. $S=\left( -\infty ;11 \right]$.

C. $S=\left( -\infty ;8 \right]$.

D. $S=\left( 2;8 \right]$.

Câu 19:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?

A. $y=-{{x}^{4}}+2{{x}^{2}}-3.$

B. $y={{x}^{3}}-3x-3$.

C. $y={{x}^{4}}-2{{x}^{2}}-3.$

D. $y=-{{x}^{3}}+3x.$

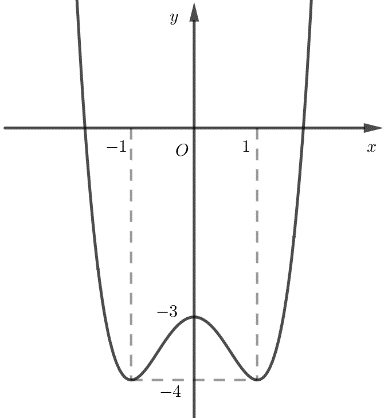
Câu 20:

Cho khối chóp có diện tích đáy $B=6$ và chiều cao $h=2.$ Thể tích của khối chóp đã cho bằng

A. $12.$

B. $24.$

C. $4.$

D. $6.$

Câu 21:

Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=\ln x$, $y=0$, $x=1$, $x=e$. Mệnh đề nào dưới đây đúng?

A. $S=\pi \int\limits_{1}^{e}{{{\left( \ln x \right)}^{2}}}\,\text{d}x$.

B. $S=\int\limits_{1}^{e}{\ln x}\,\text{d}x$.

C. $S=\pi \int\limits_{1}^{e}{\ln x}\,\text{d}x$.

D. $S=\int\limits_{1}^{e}{\ln \left( 2x \right)}\,\text{d}x$.

Câu 22:

Số cách xếp $5$ người thành một hàng ngang là

A. $C_{5}^{5}$.

B. $C_{5}^{1}$.

C. $A_{5}^{1}$.

D. $5!$.

Câu 23:

Số phức liên hợp của số phức $z=-2+3i$ là

A. $\bar{z}=2-3i$.

B. $\bar{z}=-2-3i$.

C. $\bar{z}=3-2i$.

D. $\bar{z}=2+3i$.

Câu 24:

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ:

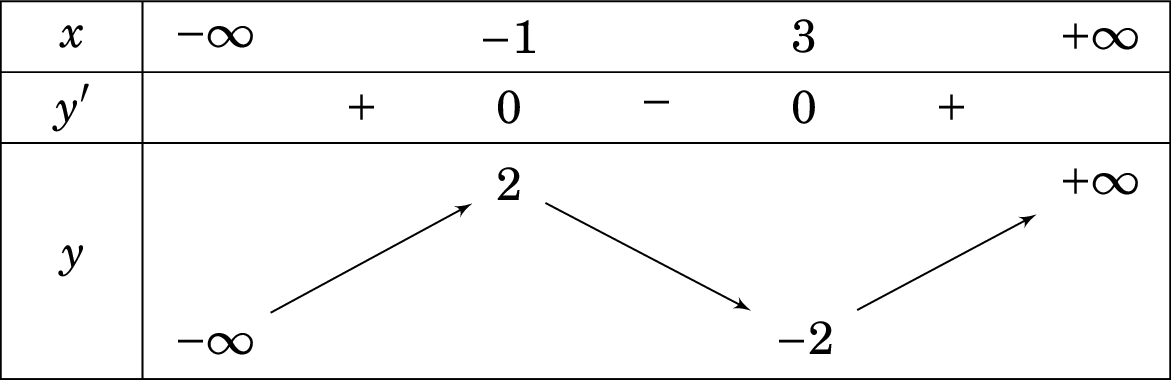
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $\left( -\infty ;2 \right)$.

B. $\left( 1;+\infty \right)$.

C. $\left( -\infty ;1 \right)$.

D. $\left( 1;3 \right)$.

Câu 25:

Lấy ngẫu nhiên một số tự nhiên nhỏ hơn $100,$ xác suất để lấy được một số chia hết cho $6$ bằng

A. $\frac{4}{25}.$

B. $\frac{16}{99}.$

C. $\frac{17}{100}.$

D. $\frac{17}{99}.$

Câu 26:

Hàm số $y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}{{x}^{2}}-6x+\frac{5}{6}$ đồng biến trên khoảng

A. $\left( -2;\ 3 \right).$

B. $\left( 3;\ +\infty \right).$

C. $\left( -\infty ;\ 3 \right).$

D. $\left( -2;\ +\infty \right).$

Câu 27:

Tính tích phân $I=\int\limits_{1}^{5}{\frac{1}{\sqrt{2x-1}+1}\text{d}x}$ bằng cách đặt $u=\sqrt{2x-1}$, mệnh đề nào dưới đây đúng?

A. $I=\int\limits_{1}^{3}{\frac{u}{u+1}}\text{d}u\text{.}$

B. $I=\int\limits_{1}^{3}{\frac{2u}{u+1}}\text{d}u.$

C. $I=\frac{1}{2}\int\limits_{1}^{5}{\frac{u}{u+1}}\text{d}u.$

D. $I=\int\limits_{1}^{5}{\frac{u}{u+1}}\text{d}u.$

Câu 28:

Cho ba điểm $A\left( 1;2;-1 \right),\,\,B\left( 2;-1;3 \right),\,\,C\left( -3;5;1 \right).$ Tìm tọa độ điểm $D$ sao cho $ABCD$ là hình bình hành.

A. $D=\left( -2\,;2\,;5 \right).$

B. $D=\left( -4\,;8\,;-5 \right).$

C. $D=\left( -2\,;8\,;-3 \right).$

D. $D=\left( -4\,;8\,;-3 \right).$

Câu 29:

Cho hai số phức ${{z}_{1}}=3+i$ và ${{z}_{2}}=2-i.$ Tính $T=\left| {{z}_{1}}+{{z}_{1}}{{z}_{2}} \right|.$

A. $T=10.$

B. $T=85.$

C. $T=50.$

D. $T=5.$

Câu 30:

Trong không gian $Oxyz,$ cho hai điểm $A\left( 1;-2;-3 \right),\,\,B\left( -1;4;1 \right)$ và đường thẳng $d:\frac{x+2}{1}=\frac{y-2}{-1}=\frac{z+3}{2}.$ Phương trình đường thẳng $\Delta $ đi qua trung điểm của đoạn $AB$ và song song với đường thẳng $d$ là

A. $\Delta :\frac{x}{1}=\frac{y-2}{-1}=\frac{z+2}{2}.$

B. $\Delta :\frac{x}{1}=\frac{y-1}{-1}=\frac{z+1}{2}.$

C. $\Delta :\frac{x-1}{1}=\frac{y-1}{-1}=\frac{z+1}{2}.$

D. $\Delta :\frac{x}{1}=\frac{y-1}{1}=\frac{z+1}{2}.$

Câu 31:

Giá trị lớn nhất của hàm số $y={{x}^{3}}-3{{x}^{2}}-9x+25$ trên đoạn $\left[ -2;2 \right]$ bằng

A. $23\cdot $

B. $30\cdot $

C. $2\cdot $

D. $-1\cdot $

Câu 32:

Cho hàm số $y=f\left( x \right)$ có đồ thị $y={f}'\left( x \right)$ cắt trục $Ox$ tại ba điểm có hoành độ $a,b,c$ như hình vẽ. Mệnh đề nào dưới đây đúng?

A. $f\left( a \right)>f\left( b \right)>f\left( c \right).$

B. $\left( f\left( b \right)-f\left( a \right) \right)\left( f\left( b \right)-f\left( c \right) \right)<0.$

C. $f\left( c \right)+f\left( a \right)-2f\left( b \right)>0.$

D. $f\left( c \right)>f\left( b \right)>f\left( a \right).$

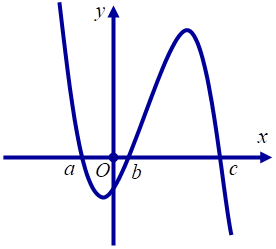
Câu 33:

Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh bằng $a$. Gọi $M$ là trung điểm $SD$ khi đó $\sin \left( CM,\left( ABCD \right) \right)$ bằng

A. $\frac{2\sqrt{5}}{5}\cdot $

B. $\frac{\sqrt{30}}{6}\cdot $

C. $\frac{\sqrt{5}}{5}\cdot $

D. $\frac{\sqrt{6}}{6}\cdot $

Câu 34:

Tổng các nghiệm của phương trình ${{\log }_{\sqrt{2}}}\left( x-1 \right)+\log \left( x+3 \right)=1$ bằng

A. $6\cdot $

B. $-5\cdot $

C. $5\cdot $

D. $4\cdot $

Câu 35:

Cho hàm số đa thức bậc bốn $y=f\left( x \right)$, đồ thị của hàm số $y={f}'\left( 1-x \right)$ là đường cong ở hình vẽ.

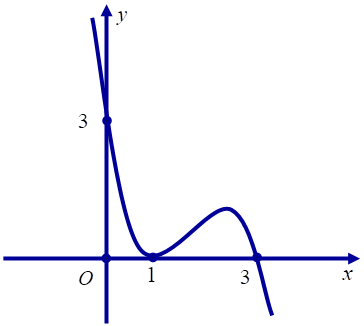
Hàm số $h\left( x \right)=f\left( x \right)-\frac{3}{2}{{x}^{2}}$ đạt giá trị nhỏ nhất trên $\left[ 0;2 \right]$ tại

A. $x=\frac{1}{2}.$

B. $x=2.$

C. $x=1.$

D. $x=0.$

Câu 36:

Cho hình lăng trụ tam giác đều $ABC.{A}'{B}'{C}'$ có cạnh đáy bằng $a,$ cạnh bên bằng $a\sqrt{2}.$ Gọi $M$ là trung điểm cạnh $AC.$ Khi đó khoảng cách từ $A$ đến mặt phẳng $\left( {A}'BM \right)$ bằng

A. $\frac{a\sqrt{2}}{3}.$

B. $\frac{a}{\sqrt{5}}.$

C. $\frac{a\sqrt{3}}{2}.$

D. $\frac{a\sqrt{5}}{3}.$

Câu 37:

Cho hàm số $y=f(x)$ có đạo hàm là ${f}'(x)=\ln \left( x+a \right),\forall x>-a,\,\ a$ là số thực dương và $f(0)=a\ln a$. Biết $\int\limits_{0}^{a}{f\left( x \right)\text{d}x}=0,$ khi đó mệnh đề nào sau đây đúng?

A. $a\in \left( 2;e \right).$

B. $a\in \left( 0;1 \right).$

C. $a\in \left( 1;\sqrt{2} \right).$

D. $a\in \left( \frac{e}{2};2 \right).$

Câu 38:

Cho $g\left( x \right)={{x}^{2}}-2x-1$ và hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ:

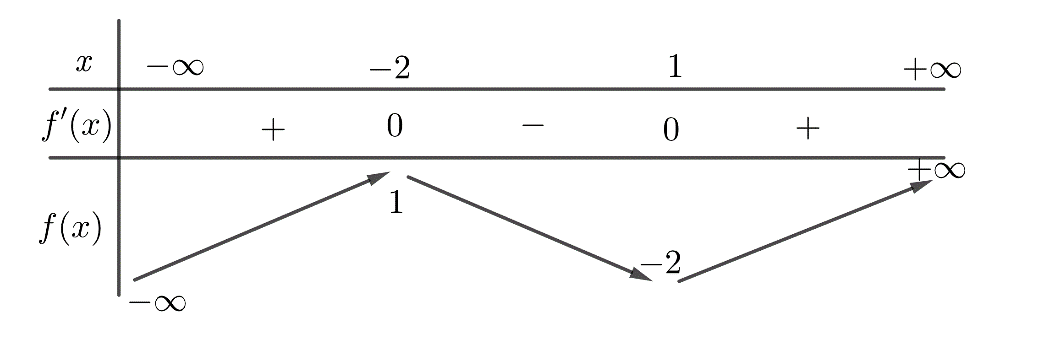
Số nghiệm của phương trình $f\left[ g\left( x \right) \right]=0$ là

A. $5.$

B. $4.$

C. $2.$

D. $6.$

Câu 39:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AD=2\sqrt{2},\,\,AB=1,\,\,$

$SA=SB,\,$$SC=SD.$ Biết rằng hai mặt phẳng $\left( SAB \right)$ và $\left( SCD \right)$ vuông góc với nhau và tổng diện tích của hai tam giác $SAB$ và $SCD$ bằng $\sqrt{3}.$ thể tích của khối chóp $S.ABCD$ bằng

A. $1.$

B. $\frac{4\sqrt{2}}{3}.$

C. $\frac{2}{3}.$

D. $\sqrt{2}.$

Câu 40:

Cho hàm số $y=f\left( x \right)$, hàm số $y={f}'\left( x \right)$ liên tục trên $R$ và có đồ thị như hình vẽ.

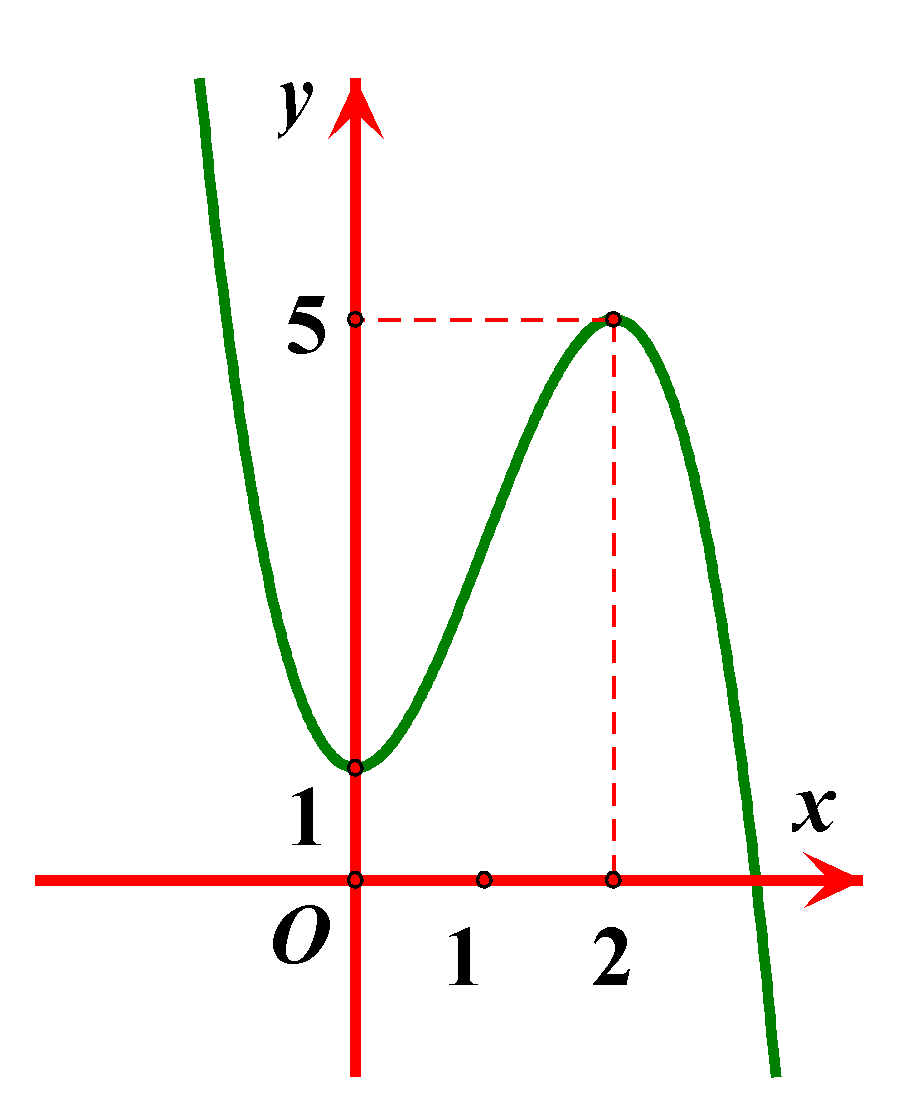
Bất phương trình $f\left( x \right)-{{\left( x-1 \right)}^{3}}>m+5x+1$ (với $m$ là tham số thực) nghiệm đúng với mọi $x\in \left( 0\,;\,3 \right)$ khi và chỉ khi

A. $m<f\left( 3 \right)-24$.

B. $m<f\left( 0 \right)$.

C. $m\le f\left( 3 \right)-24$.

D. $m\le f\left( 0 \right)$.

Câu 41:

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ:

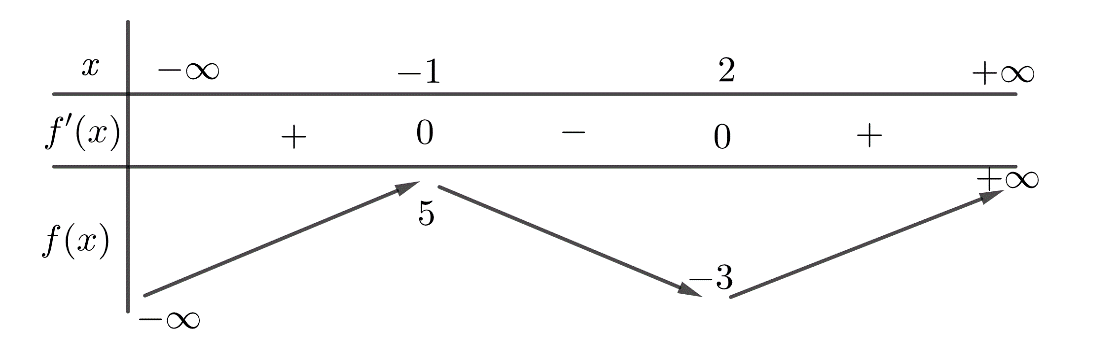
Số giá trị nguyên của tham số $m$ để hàm số $g\left( x \right)=f\left[ f\left( x \right)-m+1 \right]$ có đúng $6$ điểm cực trị là

A. $8.$

B. $10.$

C. $6.$

D. $12.$

Câu 42:

Cho hai số phức ${{z}_{1}},\,\,{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}}+2-i \right|+\left| {{z}_{1}}-4-7i \right|=6\sqrt{2}$ và $\left| i{{z}_{2}}-1+2i \right|=1.$ Giá trị nhỏ nhất của biểu thức $P=\left| {{z}_{1}}+{{z}_{2}} \right|$ bằng

A. $\text{3}\sqrt{2}-2.$

B. $\text{2}\sqrt{2}-2.$

C. $\text{3}\sqrt{2}-1.$

D. $\text{2}\sqrt{2}-1.$

Câu 43:

Cho hình nón đỉnh $S,$ đáy là hình tròn tâm $O,$ góc ở đỉnh của hình nón là $\varphi =120{}^\circ .$ Cắt hình nón bởi mặt phẳng đi qua đỉnh $S$ được thiết diện là tam giác vuông $SAB,$ trong đó $A,B$ thuộc đường tròn đáy. Biết rằng khoảng cách giữa $SO$ và $AB$ bằng $3.$ Diện tích xung quanh của hình nón bằng

A. $\text{36}\sqrt{3}\pi .$

B. $\text{18}\sqrt{3}\pi .$

C. $\text{27}\sqrt{3}\pi .$

D. $\text{9}\sqrt{3}\pi .$

Câu 44:

Trong không gian $Oxyz,$cho mặt phẳng $\left( P \right):2x-y+z-10=0$ và $d:\frac{x+2}{2}=\frac{y-1}{1}=\frac{z-1}{-1}.$ Đường thẳng $\Delta $ cắt $\left( P \right)$ và đường thẳng $d$ lần lượt tại $M$và $N$ sao cho $A\left( 1;3;2 \right)$là trung điểm của $MN.$ Tính độ dài đoạn thẳng $MN.$

A. $MN=2\sqrt{33}.$

B. $MN=2\sqrt{66}.$

C. $MN=4\sqrt{33}.$

D. $MN=4\sqrt{66}.$

Câu 45:

Cho phương trình${{z}^{2}}+az+2{{a}^{2}}=0$, với $a$ là số thực dương. Gọi ${{z}_{1}},{{z}_{2}}$ là hai nghiệm phức của phương trình, trong đó ${{z}_{1}}$có phần ảo dương. Biết rằng $\left( 2{{z}_{1}}+{{z}_{2}} \right)\overline{{{z}_{1}}}=10+2\sqrt{7}i$. Khẳng định làm sau đây đúng?

A. $1 < a < 3$.

B. $a < 1$.

C. $5 < a < 8$.

D. $3 < a < 5$.

Câu 46:

Có bao nhiêu giá trị nguyên ${b>1}$ để với mỗi giá trị của ${b}$ có đúng 5 số nguyên $a\in \left( -10;10 \right)$ thỏa mãn ${\log _{3} \frac{2 a^{2}+3 a+b}{a^{2}-a+2} \leq a^{2}-6 a+7-b}$.

A. ${16 }$.

B. ${15 }$.

C. ${9 }$.

D. ${10 }$.

Câu 47:

Cho hàm số $f\left( x \right)={{x}^{4}}+b{{x}^{2}}+c\left( b,c\in \mathbb{R} \right)$ có đồ thị là đường cong $\left( C \right)$ và đường thẳng $\left( d \right):y=g\left( x \right)$ tiếp xúc với $\left( C \right)$ tại điểm ${{x}_{0}}=1$. Biết $\left( d \right)$ và $\left( C \right)$ còn hai điểm chung khác có hoành độ là ${{x}_{1}},{{x}_{2}}\left( {{x}_{1}}<{{x}_{2}} \right)$ và $\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\frac{g\left( x \right)-f\left( x \right)}{{{\left( x-1 \right)}^{2}}}dx=\frac{4}{3}}$. Tính diện tích hình phẳng giới hạn bởi đường cong $\left( C \right)$ và đường thẳng $\left( d \right)$.

A. $\frac{29}{5}$.

B. $\frac{28}{5}$.

C. $\frac{143}{5}$.

D. $\frac{43}{5}$.

Câu 48:

Trong không gian $Oxyz,$ cho mặt phẳng $\left( P \right):x-y+z+7=0,$ đường thẳng $d:\frac{x}{1}=\frac{y}{-2}=\frac{z}{2}$ và mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=5.$ Gọi $A,\,\,B$ là hai điểm trên mặt cầu $\left( S \right)$ và $AB=4;$ ${A}',\,\,{B}'$ là hai điểm nằm trên mặt phẳng $\left( P \right)$ sao cho $A{A}',\,\,B{B}'$ cùng song song với đường thẳng $d.$ Giá trị lớn nhất của tổng $A{A}'+\,B{B}'$ gần nhất với giá trị nào sau đây

A. $13.$

B. $11.$

C. $12.$

D. $14.$

Câu 49:

Cho hàm số bậc ba $y=f\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+\frac{1}{3}x+q$ có đồ thị $\left( C \right)$ và cắt đường thẳng $d:y=g\left( x \right)$ như hình vẽ. Biết $AB=5$, tổng tất cả các nghiệm của phương trình $f\left( x \right)-g\left( x \right)-3{{x}^{2}}=2$ là

A. $4.$

B. $2.$

C. $5.$

D. $3.$

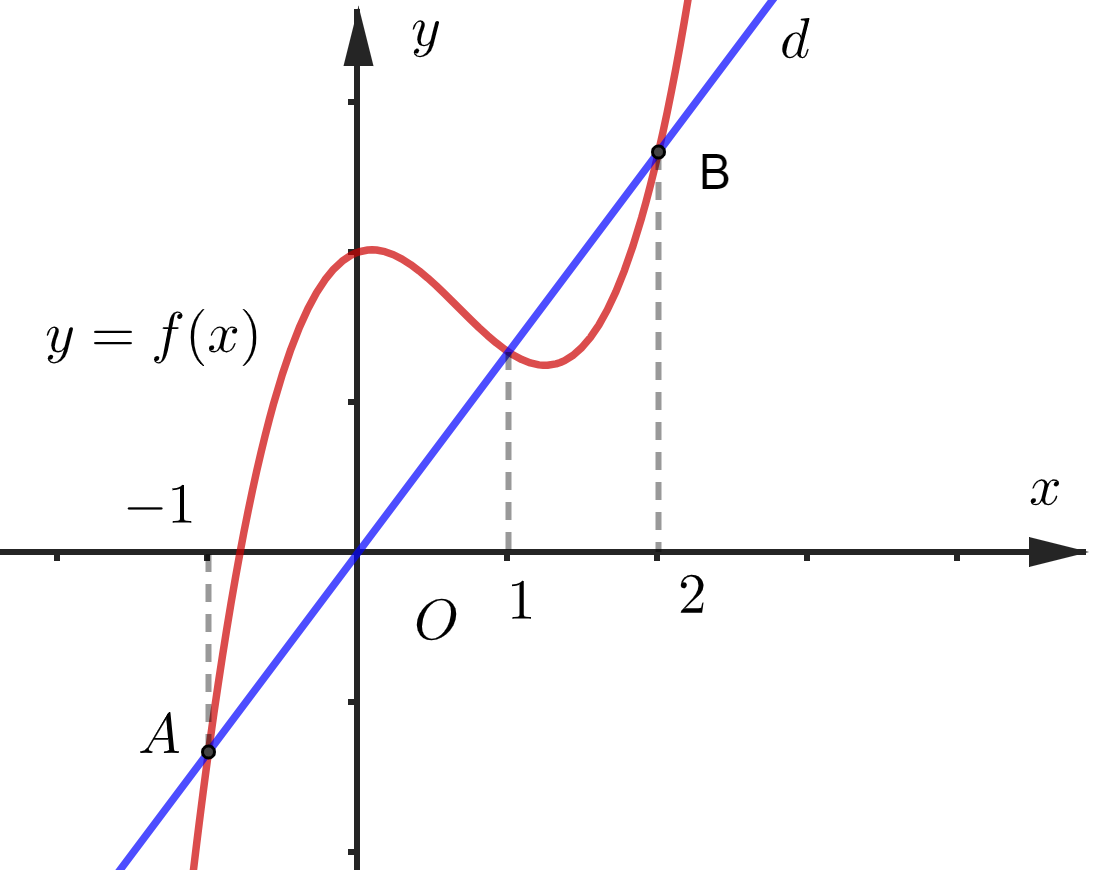
Câu 50:

Cho hàm số bậc ba $f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ dưới đây

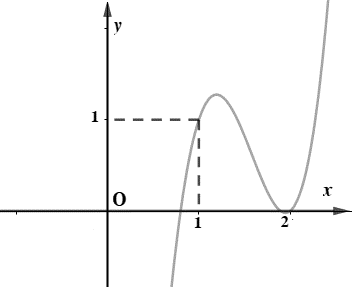
Số đường tiệm cận đứng của đồ thị hàm số $g\left( x \right)=\frac{\left( {{x}^{2}}-3x+2 \right)\sqrt{x-1}}{\left( x+1 \right)\left[ {{f}^{2}}\left( x \right)-f\left( x \right) \right]}$

A. $5$.

B. $3$.

C. $6$.

D. $4$.