Thi thử học kỳ 2 môn Toán lớp 11 online

Thí sinh đọc kỹ đề trước khi làm bài.

Tổng số câu hỏi: 0

Câu 1:

Cho cấp số nhân $\left( {{u_n}} \right)$ thỏa mãn ${u_1} = 2$ và công bội $q = - 3$. Giá trị của ${u_3}$ bằng:

A. $27$

B. $ - 27$

C. $ - 9$

D. $18$

Câu 2:

Cho cấp số cộng $\left( {{u_n}} \right)$ thỏa mãn ${u_1} = - 5$ và công sai $d = 3$. Tổng của 50 số hạng đầu tiên là:

A. $2345$

B. $6850$

C. $3425$

D. $3500$

Câu 3:

Cho cấp số nhân $\left( {{v_n}} \right)$ thỏa mãn $\left\{ \begin{array}{l}{v_2} = 2\\{v_5} = 16\end{array} \right.$. Khi đó ta có:

A. ${v_1} = - 2$

B. ${v_4} = \dfrac{1}{2}$

C. ${v_6} = 64$

D. ${v_7} = 64$

Câu 4:

Cho dãy số $\left( {{u_n}} \right)$ với $\left\{ \begin{array}{l}{u_1} = \dfrac{1}{2}\\{u_n} = \dfrac{1}{{2 - {u_{n - 1}}}},\,\,\forall n > 1\end{array} \right.$. Giá trị của ${u_4}$ bằng:

A. $\dfrac{3}{4}$

B. $\dfrac{4}{5}$

C. $\dfrac{5}{6}$

D. $\dfrac{5}{4}$

Câu 5:

Cho dãy số $\left( {{u_n}} \right)$ thỏa mãn ${u_n} = \dfrac{{2n + 1}}{{n + 1}},\,\,\forall n \ge 1$. Khẳng định nào sau đây là sai?

A. $\left( {{u_n}} \right)$ là dãy số bị chặn dưới

B. ${u_5} = \dfrac{{11}}{6}$

C. $\left( {{u_n}} \right)$ là dãy giảm

D. $\left( {{u_n}} \right)$ là dãy tăng và bị chặn

Câu 6:

Với số thực $a$ cho trước, giá trị của $\lim \dfrac{{a.n + 2}}{{2n + 1}}$ là:

A. $a$

B. $2a$

C. $\dfrac{a}{2}$

D. $1$

Câu 7:

Giá trị của $\lim \left( {\sqrt {{n^2} - 2n - 2} - n} \right)$ là:

A. $ - 1$

B. $ - \dfrac{2}{3}$

C. $ - \infty $

D. $ + \infty $

Câu 8:

Giá trị của $\lim \dfrac{{{4^n} + {6^n}}}{{{6^{n - 1}} - {5^n}}}$ là:

A. $0$

B. $ + \infty $

C. $6$

D. $\dfrac{1}{6}$

Câu 9:

Cho tứ diện $ABCD$ có $M$ là trung điểm $AB,\,\,N$ là trung điểm $AC$. Mệnh đề nào sau đây đúng?

A. Ba vectơ $\overrightarrow {AB} ,\,\,\overrightarrow {AC} ,\,\,\overrightarrow {AD} $ đồng phẳng

B. Ba vectơ $\overrightarrow {BA} ,\,\,\overrightarrow {CB} ,\,\,\overrightarrow {BD} $ đồng phẳng

C. Ba vectơ $\overrightarrow {BD} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {MN} $ đồng phẳng

D. Ba vectơ $\overrightarrow {AD} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {MN} $ đồng phẳng

Câu 10:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$. Biết rằng $SA = SB = SC = SD$. Khẳng định nào sau đây là sai?

A. $AB//\left( {SCD} \right)$

B. $AC \bot \left( {SBD} \right)$

C. $SO \bot \left( {ABCD} \right)$

D. $AD \bot \left( {SAB} \right)$

Câu 11:

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Đường thẳng $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$, $SA = a$. Khi đó góc giữa đường thẳng $SB$ và mặt phẳng $\left( {ABC} \right)$ có số đo là:

A. ${30^0}$

B. ${45^0}$

C. ${135^0}$

D. ${60^0}$

Câu 12:

Cho hình chóp $S.ABC$. Đáy $ABC$ là tam giác vuông cân tại $B,\,\,AC = 2a$. Đường thẳng $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$, $SA = a$. Khi đó, cosin của góc tạo bởi $SC$ và mặt phẳng $\left( {SAB} \right)$ có giá trị là:

A. $\dfrac{{\sqrt {15} }}{5}$

B. $\sqrt {\dfrac{2}{5}} $

C. $\sqrt {\dfrac{2}{3}} $

D. $\dfrac{1}{{\sqrt 3 }}$

Câu 13:

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị như hình vẽ. Hỏi hàm số $f\left( x \right)$ không liên tục tại điểm nào sau đây?

A. ${x_0} = 1$.

B. ${x_0} = 2$.

C. ${x_0} = 3$.

D. ${x_0} = 0$.

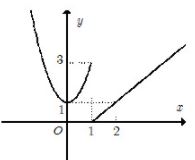
Câu 14:

Đạo hàm của hàm số $f\left( x \right) = {\left( {{x^2} + 1} \right)^4}$ tại điểm $x = - 1$ là

A. $64$.

B. $32$.

C. $ - 64$.

D. $ - 32$.

Câu 15:

Khẳng định nào sau đây là khẳng định sai?

A. Nếu $d \bot \left( \alpha \right)$ và $a//\left( \alpha \right)$ thì $a \bot d$.

B. Nếu đường thẳng $d$ vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng $\left( \alpha \right)$ thì $d$ vuông góc với bất kỳ đường thẳng nào nằm trong mặt phẳng $\left( \alpha \right)$.

C. Nếu $d \bot \left( \alpha \right)$ thì $d$ vuông góc với hai đường thẳng nằm trong $\left( \alpha \right)$.

D. Nếu đường thẳng $d$ vuông góc với hai đường thẳng trong mặt phẳng $\left( \alpha \right)$ thì $d \bot \left( \alpha \right)$.

Câu 16:

Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Các hàm đa thức liên tục trên $\mathbb{R}$.

B. Các hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng.

C. Nếu hàm số $y = f\left( x \right)$ liên tục trên khoảng $\left( {a;b} \right)$ và $f\left( a \right).\,f\left( b \right) < 0$ thì phương trình $f\left( x \right) = 0$ có ít nhất một nghiệm thuộc $\left( {a;\,b} \right)$.

D. Nếu các hàm số $y = f\left( x \right)$, $y = g\left( x \right)$ liên tục tại ${x_0}$ thì hàm số $y = f\left( x \right).g\left( x \right)$ liên tục tại ${x_0}$.

Câu 17:

Tính giới hạn $\lim \left( {\sqrt {9{n^2} + 2n} - 3n + 8} \right)$ ta được kết quả:

A. $\dfrac{{25}}{3}$ .

B. $ - \infty $.

C. $\dfrac{1}{3}$.

D. $ + \infty $ $$.

Câu 18:

Tính $\mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{2x + 1}}{{x - 3}}$ ta được kết quả.

A. $ - \infty $.

B. $ + \infty $ $$.

C. $6$.

D. $4$.

Câu 19:

Trong không gian cho tứ diện đều$\overrightarrow {AC'} = \dfrac{1}{2}\overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} $. Khẳng định nào sau đây là sai:

A. $\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} $.

B. $\overrightarrow {AD} \bot \overrightarrow {DC} $.

C. $\overrightarrow {AC} \bot \overrightarrow {BD} $.

D. $\overrightarrow {AD} \bot \overrightarrow {BC} $.

Câu 20:

Mệnh đề nào đúng trong các mệnh đề sau?

A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho (khi đường thẳng không vuông góc với mặt phẳng).

B. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường $b$ và mặt phẳng $\left( P \right)$ thì $a$ song song song hoặc trùng với $b$.

C. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường $a$ và mặt phẳng $\left( Q \right)$ thì mp$\left( P \right)$ song song với mp$\left( Q \right)$.

D. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường $b$ và mặt phẳng $\left( P \right)$ thì $a$ song song song với $b$.

Câu 21:

Mệnh đề nào đúng trong các mệnh đề sau?

A. Góc giữa hai đường thẳng $a$ và $b$ bằng góc giữa hai đường thẳng $a$ và $c$ thì $b$ song song với $c$.

B. Góc giữa hai đường thẳng bằng góc giữa hai vec tơ chỉ phương của hai đường thẳng đó.

C. Góc giữa hai đường thẳng là góc nhọn.

D. Góc giữa hai đường thẳng $a$ và $b$ bằng góc giữa hai đường thẳng $a$ và $c$ khi $b$ song song hoặc trùng với $c$.

Câu 22:

Biết $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + ax} - 1}}{x} = 3,\,\,\,\,\left( {a \in \mathbb{R}} \right)$, tìm giá trị của $a$?

A. $a = 3$.

B. $a = 0$ $$.

C. $a = 6$.

D. $a = 4$.

Câu 23:

Cho $\mathop {\lim }\limits_{x \to \,{x_0}} f\left( x \right) = L;$ $\,\mathop {\lim }\limits_{x \to \,{x_0}} g\left( x \right) = M$, với $L,M \in \mathbb{R}$. Chọn khẳng định sai.

A. $\mathop {\lim }\limits_{x \to \,{x_0}} \left[ {f\left( x \right) - g\left( x \right)} \right] = L - M$.

B. $\mathop {\lim }\limits_{x \to \,{x_0}} \left[ {f\left( x \right).g\left( x \right)} \right] = L.M$.

C. $\mathop {\lim }\limits_{x \to \,{x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = \dfrac{L}{M}$.

D. $\mathop {\lim }\limits_{x \to \,{x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M$.

Câu 24:

Cho đồ thị của hàm số $f\left( x \right)$ trên khoảng $\left( {a;\,\,b} \right)$. Biết rằng tiếp tuyến của đồ thị hàm số $f\left( x \right)$ tại các điểm ${M_1};\,\,{M_2};\,\,{M_3}$ như hình vẽ.

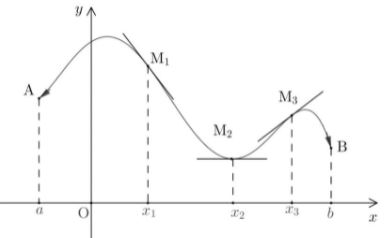
Khi đó xét dấu $f'\left( {{x_1}} \right)\,,f'\left( {{x_2}} \right)\,,f'\left( {{x_3}} \right)$.

A. $f'\left( {{x_1}} \right) = 0,\,\,f'\left( {{x_2}} \right) < 0,\,\,f'\left( {{x_3}} \right) > 0$.

B. $f'\left( {{x_1}} \right) < 0,\,\,f'\left( {{x_2}} \right) > 0,\,\,f'\left( {{x_3}} \right) = 0$.

C. $f'\left( {{x_1}} \right) < 0,\,\,f'\left( {{x_2}} \right) = 0,\,\,f'\left( {{x_3}} \right) > 0$.

D. $f'\left( {{x_1}} \right) > 0,\,\,f'\left( {{x_2}} \right) = 0,\,\,f'\left( {{x_3}} \right) < 0$.

Câu 25:

Tính giới hạn $\lim \dfrac{{{5^n} - {{3.4}^n}}}{{{{6.7}^n} + {8^n}}}$ ta được kết quả:

A. $ - \infty $.

B. $0$.

C. $\dfrac{1}{6}$.

D. $ + \infty $ $$.

Câu 26:

Tìm $a$ để hàm số $f\left( x \right) = \left\{ \begin{array}{l}{x^2} + ax + 2{\rm{ khi }}x > 1\\2{x^2} - x + 3a{\rm{ khi }}x \le 1\end{array} \right.$ có giới hạn tại $x = 1$.

A. $a = 0$ $$.

B. $a = 1$.

C. $a = 4$.

D. $a = 3$.

Câu 27:

Trong không gian cho đường thẳng $\Delta $ và điểm $O$. Qua $O$ có bao nhiêu đường thẳng vuông góc với $\Delta $?

A. 1.

B. Vô số.

C. 2.

D. 3.

Câu 28:

Cho hàm số $y = {x^3} - 3{x^2} + 2$ có đồ thị $\left( C \right)$. Tiếp tuyến của đồ thị $\left( C \right)$ tại điểm có hoành độ bằng 3 có dạng $ax + by - 25 = 0$. Khi đó, tổng $a + b$ bằng:

A. $8$.

B. $ - 10$.

C. $ - 8$.

D. $10$.

Câu 29:

Trong không gian cho hai đường thẳng $CC'$ và $b$ lần lượt có vectơ chỉ phương là $\overrightarrow u ,\,\,\overrightarrow v $. Gọi $\alpha $ là góc giữa hai đường thẳng $a$ và $b$. Khẳng định nào sau đây là đúng:

A. $\cos \alpha = \cos \left( {\overrightarrow u ;\overrightarrow v } \right)$

B. $\overrightarrow u .\overrightarrow v = \sin \alpha $.

C. $\alpha = \left| {\left( {\overrightarrow u ,\overrightarrow v } \right)} \right|$

D. $\cos \alpha = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right|$

Câu 30:

Hình hộp chữ nhật có 3 kích thước là $2;\,\,3;\,\,4$ thì độ dài đường chéo của nó là

A. $\sqrt {29} $

B. $\sqrt {30} $

C. $5$

D. $\sqrt {28} $

Câu 31:

Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 4} - 2}}{x}\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x > 0\\m{x^2} + 2m + \dfrac{1}{4}\,\,\,{\rm{khi}}\,\,x \le 0\end{array} \right.$, với $m$ là tham số. Gọi ${m_0}$ là giá trị của tham số $m$ để hàm số $f\left( x \right)$ liên tục tại $x = 0$. Hỏi ${m_0}$ thuộc khoảng nào dưới đây?

A. $\left( { - \dfrac{3}{2}; - \dfrac{1}{4}} \right)$.

B. $\left( {\dfrac{1}{2};1} \right)$.

C. $\left( { - \dfrac{1}{4};\dfrac{1}{2}} \right)$.

D. $\left( {1;2} \right)$.

Câu 32:

Cho hàm số $y = f\left( x \right) = \sqrt {x - 1} $. Trong các mệnh đề sau đây, có bao nhiêu mệnh đề đúng?

I. Hàm số $f\left( x \right)$ có tập xác định là $\left[ {1; + \infty } \right)$.

II. Hàm số $f\left( x \right)$ liên tục trên $\left[ {1; + \infty } \right)$.

III. Hàm số $f\left( x \right)$ gián đoạn tại $x = 1$.

IV. Hàm số $f\left( x \right)$ liên tục tại $x = 0$ .

A. 0

B. 1

C. 2

D. 3

Câu 33:

Cho tứ diện $ABCD$ với trọng tâm $G$. Chọn mệnh đề đúng

A. $\overrightarrow {AG} = \dfrac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BD} } \right)$

B. $\overrightarrow {AG} = \dfrac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {CD} } \right)$

C. $\overrightarrow {AG} = \dfrac{1}{4}\left( {\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BD} } \right)$

D. $\overrightarrow {AG} = \dfrac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)$

Câu 34:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh $SA = a\sqrt 3 $, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Góc giữa đường thẳng $CD$ và mặt phẳng $\left( {SBC} \right)$ là:

A. ${90^o}$

B. ${45^o}$

C. ${30^o}$

D. ${60^0}$

Câu 35:

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3$. Tính $\mathop {\lim }\limits_{x \to 2} \dfrac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}$

A. $36$

B. $27$

C. $\dfrac{{27}}{2}$

D. $4$

Câu 36:

Tìm tất cả các giá trị của tham số $m$ để phương trình $\left( {2{m^2} - 5m + 2} \right){\left( {x - 1} \right)^{18}}\left( {{x^{81}} - 2} \right) + 2x + 3 = 0$ có nghiệm:

A. $m \in \mathbb{R}$.

B. $m \in \mathbb{R}\backslash \left\{ {\dfrac{1}{2}\,;\,2} \right\}$

C. $m \in \left\{ {\dfrac{1}{2}\,;\,2} \right\}$.

D. $m \in \left\{ {0;\dfrac{1}{2}\,;\,2} \right\}$.

Câu 37:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi, cạnh bên $SA = AB$ và $SA$ vuông góc với $BC$. Góc giữa hai đường thẳng $SD$ và $BC$ là?

A. ${45^o}$

B. ${30^o}$

C. ${60^0}$

D. ${90^o}$

Câu 38:

Tính các giới hạn sau: $\mathop {\lim }\limits_{x \to 1} \dfrac{{{x^3} - 3{x^2} + 2}}{{{x^2} - 4{\rm{x}} + 3}}$

A. $\dfrac{1}{2}$

B. $\dfrac{1}{3}$

C. $\dfrac{3}{2}$

D. $\dfrac{2}{3}$

Câu 39:

Tính đạo hàm của hàm số sau: $y = \dfrac{{{x^2} + 2x - 1}}{{x + 1}}$

A. $\dfrac{{2{{\rm{x}}^2} + 4{\rm{x}} + 3}}{{{{\left( {x + 1} \right)}^2}}}$

B. $\dfrac{{{{\rm{x}}^2} + 4{\rm{x}} + 3}}{{{{\left( {x + 1} \right)}^2}}}$

C. $\dfrac{{2{{\rm{x}}^2} + 4{\rm{x}} + 3}}{{{{\left( {x - 1} \right)}^2}}}$

D. $\dfrac{{2{{\rm{x}}^2} + 4{\rm{x}} - 3}}{{{{\left( {x + 1} \right)}^2}}}$

Câu 40:

Tính giới hạn sau: $\mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt {{x^2} + 2{\rm{x}}} - 2\sqrt {{x^2} + x} + x} \right)$.

A. $ \dfrac{1}{4}$

B. $- \dfrac{1}{4}$

C. $- \dfrac{1}{6}$

D. $\dfrac{1}{6}$