Thi thử học kỳ 1 môn Toán lớp 11 online

Câu 1:

Tập xác định của hàm số $y=\frac{2{{\sin }^{2}}+3}{\cot x+\sqrt{3}}$ là:

A. $D=R\backslash \left\{ k\pi ,k\in Z \right\}$

B. $D=R\backslash \left\{ 3 \right\}$

C. $D=R\backslash \left\{ -\frac{\pi }{6}+k\pi ,k\in Z \right\}$

D. $D=R\backslash \left\{ k\pi ,-\frac{\pi }{6}+k\pi ,k\in Z \right\}$

Câu 2:

Tập giá trị của hàm số $y=\left| \tan 2x+\cot 2x \right|$ là:

A. $\left[ 2;+\infty \right)$

B. Đáp số khác

C. $\left[ -2;2 \right]$

D. R

Câu 3:

Hàm số $y={{\cos }^{2}}x$ tuần hoàn với chu kỳ là:

A. ${{\pi }^{2}}$

B. $\pi $

C. $2\pi $

D. $4\pi $

Câu 4:

Cho hàm số $y=3-5{{\sin }^{2}}x$, GTLN của hàm số là

A. 2

B. 4

C. 3

D. 5

Câu 5:

Trong hình sau thì đường nét liền và nét đứt lần lượt là đồ thị của hàm số:

A. $y=\sin x,y=-\sin x$

B. $y=-\sin x,y=\cos x$

C. $y=\cos x,y=-\cos x$

D. $y=-\sin x,y=-\cos x$

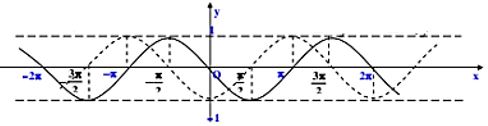
Câu 6:

Nghiệm của phương trình $2\sin \left( 2x-\frac{\pi }{6} \right)+1=0$ là:

A. $x=-\frac{\pi }{6}+k\pi ,x=\frac{7\pi }{6}+k\pi ,\,\,k\in Z$

B. $x=k\pi ,x=\frac{2\pi }{3}+k\pi ,\,\,k\in Z$

C. $x=\pm \frac{\pi }{6}+k\pi ,\,\,k\in Z$

D. $x=-\frac{\pi }{6}+k\pi ,x=\frac{2\pi }{3}+k\pi ,\,\,k\in Z$

Câu 7:

Số nghiệm của phương trình $2\cos 2x+\sqrt{3}=0$ thuộc khoảng $\left( -\frac{\pi }{2};\frac{\pi }{2} \right)$ là:

A. 1

B. 2

C. 3

D. 4

Câu 8:

Nghiệm của trương trình $\sin 4x=2\cos 2x$ là:

A. $x=\frac{\pi }{4}+\frac{k\pi }{2},\,\,k\in Z$

B. $x=k\pi ,\,\,k\in Z$

C. $x=\frac{\pi }{4}+k\pi ,\,\,k\in Z$

D. $x=\frac{k\pi }{2},\,\,k\in Z$

Câu 9:

Nghiệm của phương trình $\tan 2x+\cot x=0$ là:

A. $x=\frac{\pi }{2}+k2\pi ,\,\,k\in Z$

B. $x=\frac{\pi }{2}+k\pi ,\,\,k\in Z$

C. Vô nghiệm

D. Đáp số khác

Câu 10:

Nghiệm của phương trình $\cos 2x=2\sin x+1$ là:

A. $x=\frac{\pi }{2}+k\pi ,x=k2\pi ,\,\,k\in Z$

B. $x=k\pi ,x=-\frac{\pi }{2}+k2\pi ,\,\,k\in Z.$

C. $x=\pm \frac{\pi }{2}+k\pi ,\,\,k\in Z$

D. Vô nghiệm.

Câu 11:

Định m để phương trình ${{\cos }^{2}}x-2m\cos x+4\left( m-1 \right)=0$ có nghiệm thỏa mãn $-\frac{\pi }{2}<x<\frac{\pi }{2}$

A. $1 < m \le \frac{3}{2}$

B. $1 < m <\frac{3}{2} $

C. $-\frac{3}{2} < m <-1$

D. $-1\le m\le 1$

Câu 12:

Từ tập hơp $A=\left\{ 0;1;2;3;4;5 \right\}$ có thể lập được bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau và lớn hơn 300.000 ?

A. 5!3!

B. 5!2!

C. 5!

D. 3.5!

Câu 13:

Từ tập hợp $A=\left\{ 0;1;2;3;4;5;6;7;8;9 \right\},$ có thể lập được bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau:

A. $9A_{9}^{5}$

B. $9A_{10}^{5}$

C. $9C_{9}^{5}$

D. $A_{10}^{6}$

Câu 14:

Trong một lớp học có 30 học sinh nam và 15 học sinh nữ. Muốn thành lập đội văn nghệ gồm 6 người, trong đó có ít nhất bốn nam. Hỏi có bao nhiêu cách?

A. 412803

B. 763806

C. 2783638

D. 5608890

Câu 15:

Cho đa giác lồi có n cạnh $\left( n\ge 4 \right)$, các đường chéo của đa giác cắt nhau tạo thành bao nhiêu giao điểm, biết rằng không có ba đường thẳng nào đồng quy.

A. $C_{\frac{n\left( n-3 \right)}{2}}^{2}$

B. $C_{n}^{2}$

C. Đáp số khác

D. $C_{n}^{2}C_{n}^{4}$

Câu 16:

Nghiệm của phương trình $A_{x+1}^{3}+C_{x+1}^{x-1}=14\left( x+1 \right)$ là:

A. 3

B. 4

C. 8

D. Cả A, B, C đều đúng.

Câu 17:

Số hạng chứa ${{x}^{12}}$ trong khai triển của nhị thức ${{\left( 2{{x}^{2}}-1 \right)}^{10}}$ là:

A. $13440{{x}^{12}}$

B. $11240{{x}^{12}}$

C. $-13440{{x}^{12}}$

D. $-11240{{x}^{12}}$

Câu 18:

Tìm số hạng không chứa x trong khai triển của ${{\left( x-\frac{2}{{{x}^{3}}} \right)}^{16}}$

A. $-C_{16}^{4}{{2}^{4}}$

B. $-C_{16}^{4}{{2}^{12}}$

C. $C_{16}^{4}{{2}^{4}}$

D. $-C_{16}^{4}{{2}^{12}}$

Câu 19:

Cho biết tổng của các hệ số trong khai triển ${{\left( 1+2x \right)}^{n}}$ là 6561. Tìm n ?

A. n = 3

B. n = 4

C. n = 6

D. n = 8

Câu 20:

Tính tổng $S={{5}^{20}}C_{20}^{0}-{{5}^{19}}C_{20}^{1}+{{5}^{18}}C_{20}^{2}-...+C_{20}^{20}$

A. ${{2}^{40}}$

B. $-{{2}^{40}}$

C. ${{5}^{20}}$

D. $-{{5}^{20}}$

Câu 21:

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố: Tổng số chấm trong 2 lần gieo bằng 6 ?

A. $\frac{1}{6}$

B. $\frac{1}{9}$

C. $\frac{1}{18}$

D. $\frac{5}{36}$

Câu 22:

Một bình chứa 16 viên bi, với 7 viên bi trắng, 6 viên bi đen, 3 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi. Tính xác suất lấy được 1 viên bi trắng, 1 viên bi đen, 1 viên bi đỏ.

A. Đáp số khác

B. $\frac{1}{16}$

C. $\frac{9}{40}$

D. $\frac{143}{280}$

Câu 23:

Một lớp học gồm 15 học sinh nam và 10 học sinh nữ, giáo viên chọn ra 5 học sinh để tham gia đội văn nghệ. Tính xác suất để 5 học sinh đươc chọn có cả nam lẫn nữ và số học sinh nữ ít hơn học sinh nam.

A. $\frac{325}{506}$

B. $\frac{321}{506}$

C. $\frac{15}{253}$

D. $\frac{18}{253}$

Câu 24:

Có hai hộp cùng chứa các quả cầu. Hộp nhứ nhất có 3 quả cầu đỏ, 7 quả cầu xanh. Hộp thứ hai có 4 quả cầu đỏ, 6 quả cầu xanh. Lấy ra ngẫu nhiên 2 quả cầu trong hộp thứ nhất và 1 quả cầu trong hộp thứ hai. Tính xác suất để 3 quả cầu lấy ra cùng màu đỏ.

A. $\frac{7}{20}$

B. $\frac{5}{20}$

C. $\frac{7}{75}$

D. $\frac{2}{75}$

Câu 25:

Có 10 người khách bước ngẫu nhiên vào một cửa hàng có 3 quầy. Hỏi xác suất để 3 người cùng đến quầy số 1 là:

A. $\frac{C_{10}^{3}{{2}^{7}}}{{{3}^{10}}}$

B. $\frac{C_{10}^{3}C_{7}^{2}}{{{3}^{10}}}$

C. $\frac{C_{10}^{3}{{2}^{3}}}{{{3}^{10}}}$

D. $\frac{C_{10}^{3}{{2}^{7}}}{{{3}^{7}}}$

Câu 26:

Phép tịnh tiến theo vector $\overrightarrow{v}=\left( 5;4 \right)$ biến điểm$A\left( -1;2 \right)$ thành điểm nào trong các điểm sau đây?

A. $A'\left( 3;4 \right)$

B. $A'\left( 4;6 \right)$

C. Đáp án khác

D. $A'\left( 1;3 \right)$

Câu 27:

Trong mặt phẳng Oxy cho đường thẳng $\Delta :2x-y+3=0$. Ảnh của đường thẳng $\Delta $ qua phép tịnh tiến theo $\overrightarrow{u}\left( 2;-1 \right)$ có phương trình là:

A. $2x-y+5=0$

B. $2x-y-2=0$

C. $2x-y-3=0$

D. $2x-y-1=0$

Câu 28:

Trong hệ tọa độ Oxy cho đường thẳng $d:2x+y-3=0$, ảnh của d qua phép vị tự tâm $I\left( 2;-3 \right)$ tỉ số - 2 là:

A. $2x+y-3=0$

B. $2x+y+3=0$

C. $2x+y-1=0$

D. $2x+y+2=0$

Câu 29:

Cho tứ diện ABCD, M là trung điểm của AB, N là trung điểm của AC, P là trung điểm của AD. Đường thẳng MN song song với:

A. AB

B. BC

C. PC

D. BD

Câu 30:

Cho hai đường thẳng phân biệt không có điểm chung cùng nằm trên một mặt phẳng thì hai đường thẳng đó:

A. Song song

B. Chéo nhau

C. Cắt nhau

D. Trùng nhau

Câu 31:

Cho hình chóp S.ABCD có ABCD là hình bình hành. Gọi e là giao tuyến của các (SAB) và (SCD). Tìm e?

A. e = Sx với Sx là đường thẳng song song với hai đường thẳng AD và BC.

B. e = SI với I là giao điểm của AB và MD, với M là trung điểm của BD.

C. e = SO với O là giao điểm của hai đường thẳng AC và BD.

D. e = Sx với Sx là đường thẳng song song với hai đường thẳng AB và CD.

Câu 32:

Cho hình chóp $S.ABCD$ với đáy $ABCD$ là tứ giác có các cặp cạnh đối không song song. Giả sử $AC$ và $BD$ cắt nhau tại $I$. $AD$ và $BC$ cắt nhau tại $O$. Giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$ là:

A. $SC$

B. $SB$

C. $SO$

D. $SI$

Câu 33:

Cho hình chóp S.ABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho SN = 2NB, O là giao điểm của AC và BD. Giao điểm của MN với (ABCD) là điểm K. Hãy chọn cách xác định điểm K đúng nhất trong bốn phương án sau:

A. K là giao điểm của MN và SO

B. K là giao điểm của MN với BC

C. K là giao điểm của MN với AB

D. K là giao điểm của MN với BD

Câu 34:

Cho hình chóp S.ABCD có đáy ABCD là một tứ giác (AB và CD không song song). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho SN = 2NB, O là giao điểm của AC và BD. Giả sử đường thẳng d là giao tuyến của (SAC) và (SBD). Nhận xét nào sau đây là đúng?

A. d cắt MN

B. d cắt SO

C. d cắt AB

D. d cắt CD

Câu 35:

Cho hình chóp S.ABCD. Gọi $O=AC\cap BD.$ Một mặt phẳng $\left( \alpha \right)$ cắt SA, SB, SC, SD tại A’, B’, C’, D’. Giả sử $AB\cap CD=E,A'B'\cap C'D'=E'.$ Tìm phát biểu đúng trong các phát biểu sau:

A. S, E, E’ thẳng hàng.

B. S, E, A’ thẳng hàng

C. S, E’, A’ thẳng hàng

D. C’, E, A’ thẳng hàng

Câu 36:

Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp cắt bởi mặt phẳng $\left( \alpha \right)$ đi qua M song song với BD và AC là:

A. Hình bình hành

B. Hình thoi

C. Tam giác

D. Hình thang cân

Câu 37:

Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mặt phẳng qua M và song song với (SIC). Thiết diện tạo bởi (P) và tứ diện S.ABC là:

A. Hình thoi

B. Hình bình hành

C. Tam giác cân tại M

D. Tam giác đều

Câu 38:

Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( \alpha \right)$ qua O song song với AB và SC là hình gì?

A. Hình vuông

B. Hình bình hành

C. Hình chữ nhật

D. Hình thang

Câu 39:

Cho tứ diện ABCD có các cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:

A. $\frac{{{\left( a+m \right)}^{2}}\sqrt{3}}{4}$

B. $\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}$

C. $\frac{{{\left( a-m \right)}^{2}}\sqrt{2}}{2}$

D. $\frac{{{m}^{2}}\sqrt{3}}{4}$

Câu 40:

Cho tứ diện ABCD. Gọi E, F, G lần lượt nằm trên ba cạnh AB, BC, CD mà không trùng với các đỉnh. Thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là:

A. Một tứ giác

B. Một tam giác

C. Một ngũ giác

D. Một đoạn thẳng