Đề thi thử tốt nghiệp THPT môn Toán năm 2023 - Trường THPT Nguyễn Bỉnh Khiêm

Phương trình ${{\log }_{2}}(x-5)=5$ có nghiệm là

Tập xác định của hàm số $y={{({{x}^{3}}+27)}^{\frac{\pi }{2}}}$ là

Cho cấp số nhân $({{u}_{n}})$ có ${{u}_{1}}=2,\text{ }{{u}_{4}}=-54$. Tìm công bội $q$.

Câu 4:

Cho hàm đa thức bậc bốn $y=f(x)$ có đồ thị như hình bên dưới.

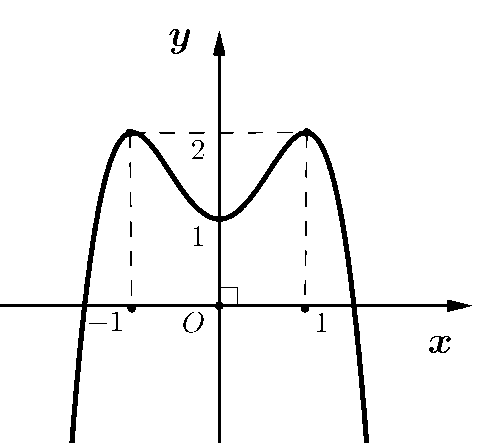
Khẳng định nào đúng?

Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ a;b \right]$. Gọi $D$ là hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$, trục hoành và hai đường thẳng $x=a,\ x=b$. Thể tích khối tròn xoay được tạo thành khi quay $D$ quanh trục hoành được tính theo công thức

Môđun của số phức $z=\left( -4+3i \right).i$ bằng

Câu 7:

Cho số phức $z=-2+i$. Trong hình dưới, điểm biểu diễn số phức $\overline{z}$ là

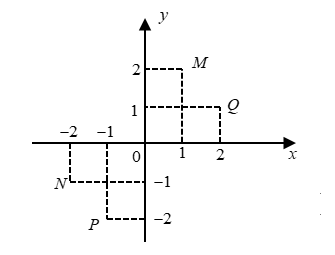
Cho số phức $z=1-2i$. Phần ảo của số phức $\overline{z}$ là?

Có bao nhiêu số tự nhiên gồm $4$ chữ số đôi một khác nhau lập ra từ các chữ số $2$, $4$, $6$, $8$?

Câu 10:

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

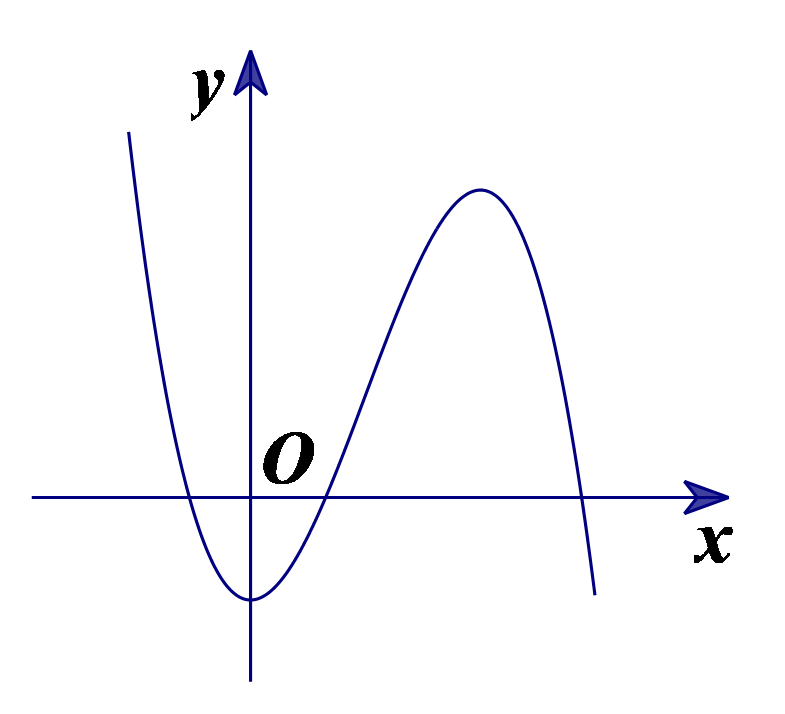
Tìm họ các nguyên hàm của hàm số $y={{e}^{x}}+2x$.

Tìm đường tiệm cận ngang của đồ thị hàm số $y=\frac{3x-4}{x-1}$.

Giá trị cực tiểu của hàm số $y=-{{x}^{3}}+3x+4$ là

Cho $\int\limits_{-2}^{2}{f\left( x \right)dx}=9$ và $\int\limits_{1}^{2}{f\left( x \right)dx}=2$ thì $\int\limits_{-2}^{1}{f\left( x \right)\text{d}x}$ bằng

Câu 15:

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

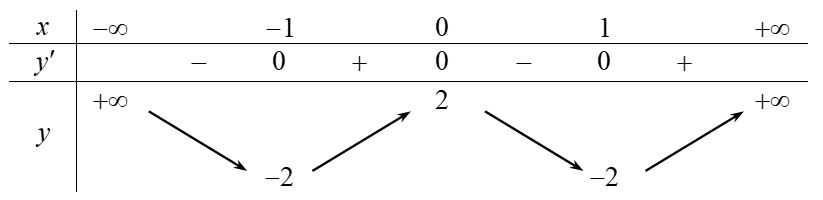
Phương trình $f\left( x \right)=0$ có bao nhiêu nghiệm?

Gọi $m,M$ lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số $y=x-\ln x$ trên đoạn $\left[ \frac{1}{2};e \right]$. Giá trị của $M-m$ là

Trong không gian $Oxyz$, hình chiếu vuông góc của điểm $M(3;-1;1)$ trên trục $Oz$ có tọa độ là

Trong không gian $Oxyz$, điểm nào sau đây thuộc đường thẳng $d:\frac{x}{2}=\frac{y+1}{-3}=\frac{z}{1}$

Trong không gian $Oxyz$, mặt phẳng $(\alpha ):5x-7y-z+2=0$ nhận vectơ nào sau đây làm vectơ pháp tuyến?

Một hộp chứa 7 quả cầu xanh, 5 quả cầu vàng (các quả cầu đôi một khác nhau). Chọn ngẫu nhiên 3 quả cầu từ hộp, tính xác suất để 3 quả được chọn có ít nhất 2 quả xanh.

Trong không gian $Oxyz$, cho mặt cầu $(S):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x+2y+1=0$. Tâm của mặt cầu $(S)$ có tọa độ là
 

Phương trình ${{z}^{2}}+az+b=0;(a,b\in \mathbb{R})$có nghiệm phức là $3+4i$. Giá trị của $a+b$bằng:

Trong không gian $Oxyz$, vectơ nào là vectơ chỉ phương của đường thẳng $d:\frac{x}{2}=\frac{y+1}{-3}=\frac{z}{1}$
 

Trong không gian cho hình chữ nhật $ABCD$ có $AB=1$ và $AD=2$. Gọi $M,N$lần lượt là trung điểm của $AD$và $BC$. Quay hình chữ nhật đó xung quanh trục MN, ta được hình trụ. Diện tích toàn phần của hình trụ bằng:

Biết $F(x)$ là một nguyên hàm của hàm số $f(x)=\frac{1}{x}$ trên $\left( 0;+\infty  \right)$ và $F(1)=1$. Tính $F(3)$

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=\frac{1}{3}{{x}^{3}}-m{{x}^{2}}-(2m-3)x-m+2$ luôn đồng biến trên $\mathbb{R}?$

Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh bằng $a$, cạnh $SA$ vuông góc với mặt đáy và
$SA=2a$. Gọi $M$ là trung điểm của cạnh $SC$, tính côsin góc $\varphi $ giữa đường thẳng $BM$ và mặt phẳng $\left( ABC \right)$

Cho hình lăng trụ đứng $ABC.{A}'{B}'{C}'$ có mặt đáy $ABC$ là tam giác vuông tại $B$ có $AB=a,\,AC=a\sqrt{3},\,{A}'B=2a$. Gọi $M$ là trung điểm của cạnh $AC$. Tính khoảng cách từ $M$ đến $\left( {A}'BC \right)$

Câu 29:

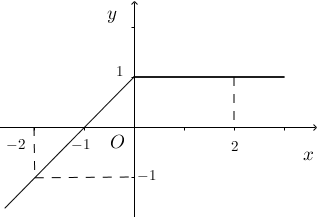
Hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên. Giá trị của $\int\limits_{-2}^{2}{f\left( x \right)dx}$ bằng

Trong không gian $Oxyz$, cho đường thẳng $d$ có phương trình $d:\,\left\{ \begin{align}
  & x=-1+t \\ 
 & y=2-3t \\ 
 & z=t \\ 
\end{align} \right.$ và điểm $A\left( 2;\,3;\,1 \right).$Mặt phẳng $\left( P \right)$ đi qua điểm $A$, vuông góc với đường thẳng $d$ có phương trình là
 

Một vật chuyển động theo quy luật $s=-\frac{1}{3}{{t}^{3}}+6{{t}^{2}}$ với $t$ (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và $s$ (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian $7$ giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bao nhiêu?
 

Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):x+3y-2z+2=0$ và đường thẳng $d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z-4}{1}$. Đường thẳng qua $A\left( 1;2;-1 \right)$ và cắt $\left( P \right)$ và $d$ lần lượt là tại $B,\,\,C\left( a;b;c \right)$ sao cho $C$ là trung điểm $AB$. Giá trị biểu thức $a+b+c$ bằng:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Cạnh bên $SA$ vuông góc với đáy, $SC=a\sqrt{3}$. Gọi $M,\,N,P,\,Q$ lần lượt là trung điểm của $SB,\,SD,CD,\,BC$. Thể tích của khối chóp$A.MNPQ$ bằng

Cho khối tứ diện $ABCD$ có thể tích $V$. Gọi $V'$ là thể tích của khối tám mặt có các đỉnh là trung điểm các cạnh của khối đa diện $ABCD$. Tính tỉ số $\frac{V'}{V}$ bằng:
 

Câu 35:

Cho hàm bậc ba $f\left( x \right)$ có đồ thị hàm số như hình vẽ bên.

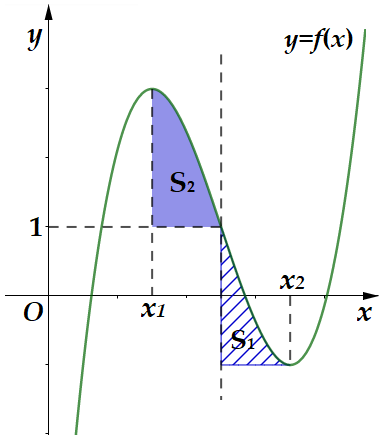
Biết hàm số $f\left( x \right)$ đạt cực trị tại hai điểm ${{x}_{1}},{{x}_{2}}$ thỏa mãn ${{x}_{2}}={{x}_{1}}+2$ và $f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right)=2$. Gọi ${{S}_{1}},{{S}_{2}}$ là diện tích của hai hình phẳng được cho trong hình vẽ bên. Tính tỉ số $\frac{{{S}_{1}}}{{{S}_{2}}}$

Cho hình chóp $S.ABC\text{D}$ có đáy $ABC\text{D}$ là hình vuông cạnh $a$. Tam giác $SAB$ vuông tại $S$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp $S.ABC\text{D}$ bằng

Trong không gian với hệ tọa độ $\text{O}xyz$, cho các điểm $A\left( 1;0;0 \right)$, $B\left( 0;2;0 \right)$,$C\left( 0;0;4 \right)$.Viết phương trình đường thẳng $\Delta $ đi qua trực tâm $H$ của tam giác $\Delta ABC$ và vuông góc với mặt phẳng $\left( ABC \right)$.

Tính tổng $T$ tất cả các nghiệm thực của phương trình ${{4.9}^{x}}-{{13.6}^{x}}+{{9.4}^{x}}=0$

Câu 39:

Cho hàm đa thức bậc ba $y=f\left( x \right)$ liên tục, có đạo hàm trên $\left[ -2;2 \right]$ và có đồ thị như hình vẽ

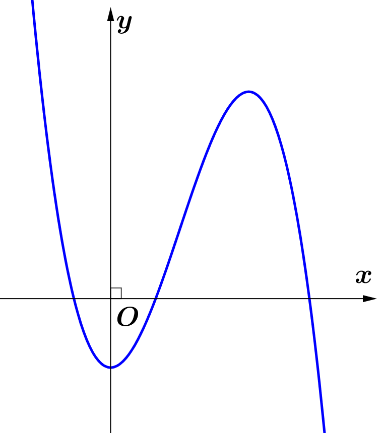
Số điểm cực tiểu của hàm số $y=\sqrt[3]{{{\left( f\left( x \right) \right)}^{2}}}$ là

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và có $f\left( -2 \right)=2;f\left( 0 \right)=1.$ Tính $I=\int\limits_{-2}^{0}{\frac{{f}'\left( x \right)-f\left( x \right)}{{{e}^{x}}}dx}.$

Tập hợp các điểm biểu diễn số phức $z$ thỏa mãn $\left| 5z \right|=\left| \left( 4+3i \right)z-25 \right|$ là đường thẳng có phương trình

Có bao nhiêu số nguyên $x$ thỏa mãn $\left[ {{3}^{2x}}-{{4.3}^{x+1}}+27 \right]\left[ {{\log }_{3}}\left( x+1 \right)+x-3 \right]\le 0$

Câu 43:

Cho hàm số đa thức bậc ba như hình vẽ.

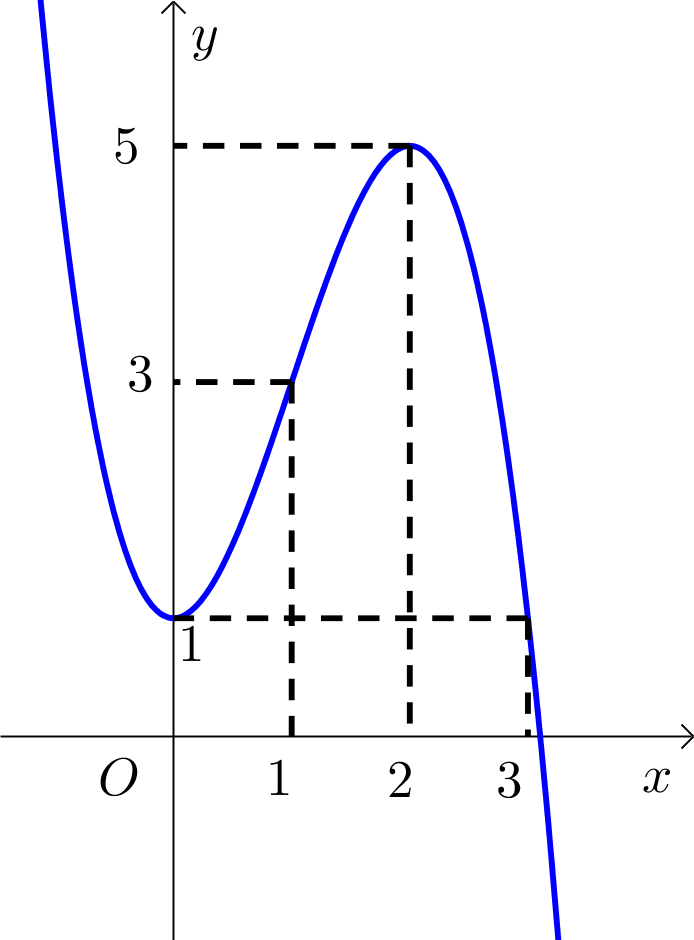
Có bao nhiêu giá trị nguyên của tham số $m$để hàm số $y=f\left( f\left( x \right)+m \right)$ có đúng $6$ điểm cực trị?

Cho hình lăng trụ ${ABC.A'B'C'}$ có $A{A}'=A{B}'=A{C}'$. Tam giác ${ABC}$ vuông cân tại ${A}$ có ${BC=2a}$. Khoảng cách từ ${A}'$ đến mặt phẳng $\left( BC{C}'{B}' \right)$ là $\frac{a\sqrt{3}}{3}$. Tính thể tích khối lăng trụ đã cho.

Câu 45:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số $m$ sao cho phương trình $2f\left( \sin x-\cos x \right)=m-1$ có hai nghiệm phân biệt trên khoảng $\left( -\frac{\pi }{4}\,;\,\frac{3\pi }{4} \right)$?

Câu 46:

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị ${f}'\left( x \right)$ như hình vẽ bên.

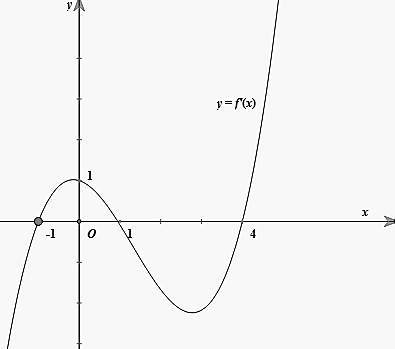
Bất phương trình ${{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)>4-m$ đúng với mọi $x\in \left( -1\,;\,4 \right)$khi và chỉ khi

Câu 47:

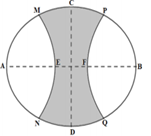
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh $A,\,B,\,C,\,D$ và hai đường parabol có các đỉnh lần lượt là $E,\,F$ (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng $AB$, đối xứng nhau qua trục $CD$, hai parabol cắt elip tại các điểm $M,\,N,\,P,\,Q$. Biết $AB=8\,m,\,CD=6\,m, $ $MN=PQ=3\sqrt{3}\,m,\,EF=2\,m$. Chi phí để trồng hoa trên vườn là $300.000$đ/${{m}^{2}}$. Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây?

Xét các số phức $\text{w}$, $z$ thỏa mãn $\left| \text{w}+i \right|=\frac{3\sqrt{5}}{5}$ và $5w=\left( 2+i \right)\left( z-4 \right)$. Tìm giá trị lớn nhất của biểu thức $P=\left| z-2i \right|+\left| z-6-2i \right|$.

Tìm tất cả các giá trị thực của tham số $m$ để phương trình $x{{\log }_{3}}\left( x+1 \right)={{\log }_{9}}\left[ 9{{\left( x+1 \right)}^{2m}} \right]$ có hai nghiệm phân biệt.

Trong không gian với hệ trục tọa độ $Oxyz$, từ điểm $A\left( 1;1;0 \right)$ ta kẻ các tiếp tuyến đến mặt cầu $\left( S \right)$ có tâm $I\left( -1;1;1 \right)$ và bán kính $R=1$. Gọi $M\left( a;b;c \right)$ là một trong các tiếp điểm ứng với các tiếp tuyến trên. Tìm giá trị lớn nhất của biểu thức $T=\left| 2a-b+2c \right|$.