Đề thi thử tốt nghiệp THPT môn toán 2025, Sở GD&ĐT Hải Dương
Phần 1: Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Tổng số câu hỏi: 0
Câu 1: Cho hàm số $ y = f(x) $ liên tục trên $ \mathbb{R} $ và có bảng xét dấu $ f'(x) $ như hình vẽ dưới đây.
Hàm số $ y = f(x) $ đồng biến trên khoảng nào dưới đây?
Câu 2: Cho hàm số $ y = f(x) $ có bảng biến thiên như hình vẽ sau đây:
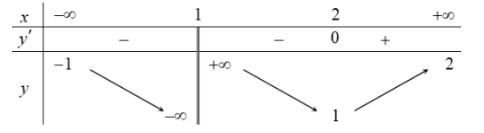Đồ thị hàm số hàm số $ y = f(x) $ có bao nhiêu đường tiệm cận?
Câu 3: Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy ( ABC). Góc tạo bởi SB và mặt phẳng ( ABC) là góc:
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Khẳng định nào sau đây đúng?
Câu 5: Trong không gian \( Oxyz \), cho hai điểm \( A(2;1;3) \), \( B(1;-1;5) \). Độ dài đoạn thẳng \( AB \) là:
Câu 6: Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, người ta thu được bảng số liệu sau:
Khoảng tứ phân vị của bảng số liệu trên gần nhất với giá trị nào dưới đây?
Câu 7: Trong không gian \( Oxyz \), cosin của góc giữa hai vectơ \( \overrightarrow{u} = (10;10;20) \), \( \overrightarrow{v} = (10;-20;10) \) là:
Câu 8: Người ta ghi lại tốc độ của 40 ô tô khi đi qua một trạm đo tốc độ và có được bảng số liệu sau:
Ghép nhóm bảng số liệu trên thành các nhóm có độ rộng bằng nhau và nhóm đầu tiên là nửa khoảng [40;45) thì khoảng biến thiên của mẫu số ghép nhóm nói trên là:
Câu 9: Tập xác định của hàm số \( y = \frac{1}{\sin x - \cos x} \) là:
Câu 10: Cho hàm số có bảng biến thiên như hình vẽ dưới đây:
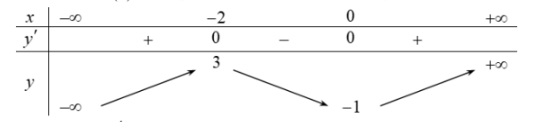Giá trị cực đại của hàm số là
Câu 11: Cho cấp số cộng \( (u_n) \) có \( u_1 = 5 \), \( u_{12} = 38 \) thì công sai là:
Câu 12: Cho khối lăng trụ có diện tích đáy \( S = 10 \text{ cm}^2 \), cạnh bên có độ dài bằng \( 10 \) cm và tạo với mặt đáy một góc bằng \( 60^\circ \). Thể tích khối lăng trụ đã cho là:
Phần 2: Câu trắc nghiệm đúng sai.Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Nếu cho 1 ý là đúng, thí sinh tích chọn đáp án. Nếu cho 1 ý là sai, thí sinh bỏ trống không chọn.
Tổng số câu hỏi: 0
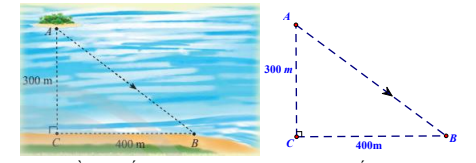
Câu 1: Trong một trò chơi thử thách, bạn Giáp đang ở trên thuyền (vị trí A) cách bờ hồ (vị trí C) 300 m và cần đi đến vị trí B trên bờ hồ như hình vẽ 1 dưới đây, khoảng cách từ C đến B là 400 m.
Lưu ý là Giáp có thể chèo thuyền thẳng từ A đến B hoặc chèo thuyền từ A đến một điểm nằm giữa C và B rồi chạy bộ đến B.
Hình 1:
Hình 2:
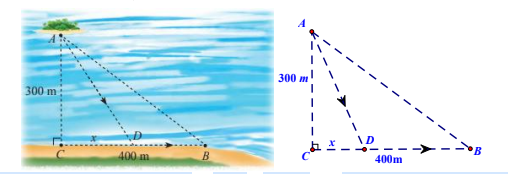
Biết rằng Giáp chèo thuyền với tốc độ 50m/phút và chạy bộ với tốc độ 100m/phút
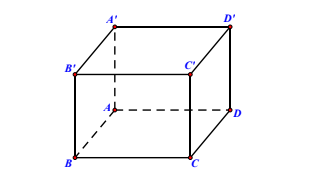
Câu 2: Trong không gian \( Oxyz \), cho hình lập phương \( ABCD.A'B'C'D' \) có cạnh bằng 1 (tham khảo hình vẽ).
Câu 3: Cho hàm số \( f(x) = 92 - 20\ln(x+1) \).
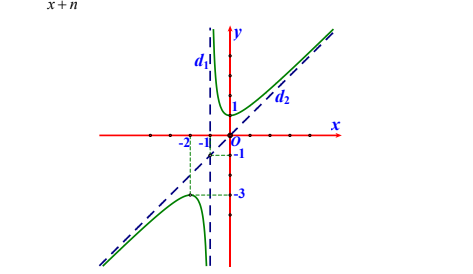
Câu 4: Cho hàm số \( y = \frac{x^2 + bx + c}{x + n} \) có đồ thị và hai đường tiệm cận \( d_1, d_2 \) như hình vẽ dưới đây.
Phần 3: Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tổng số câu hỏi: 0
Câu 1: Cho hai số thực dương \( x, y \) thỏa mãn \( 2^y + y = 2x + \log_2 (x + 2^{y-1}) \). Giá trị nhỏ nhất của biểu thức \( T = \frac{x}{y} \) bằng bao nhiêu, kết quả làm tròn đến hàng phần trăm?
Câu 2: Trong không gian \( Oxyz \), cho điểm \( A(2;3;-1) \), \( B(-8;7;-3) \) và điểm \( M(a;b;c) \) thuộc mặt phẳng \( (Oxy) \). Biết rằng \( A,B,M \) thẳng hàng, hãy tính \( 2a - b + 3c \).
Câu 3: Một chiếc máy có 3 động cơ \( I \), \( II \) và \( III \) chạy độc lập nhau. Khả năng để động cơ \( I \), \( II \) và \( III \) hoạt động tốt trong ngày lần lượt là 70%, 80% và 85%. Xác suất để có ít nhất 1 động cơ chạy tốt trong ngày là bao nhiêu phần trăm?
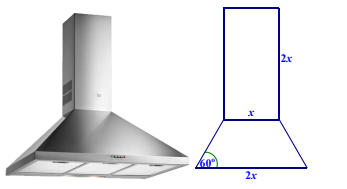
Câu 4: Một ống khối có cấu trúc gồm một khối chóp cụt tứ giác đều có thể tích \(V_1\) và một khối hộp chữ nhật có thể tích \(V_2\) ghép lại với nhau như hình vẽ bên dưới. Cho biết bản vẽ hình chiếu của ống khối với phương chiếu trùng với phương của một cạnh đáy khối chóp cụt, hãy tính tỉ số thể tích \( \frac{V_1}{V_2} \), kết quả làm tròn đến hàng phần trăm.
Câu 5: Một xí nghiệp \( A \) chuyên cung cấp sản phẩm \( S \) cho nhà phân phối \( B \). Hai bên thỏa thuận rằng, nếu đầu tháng \( B \) đặt hàng \( x \) tạ sản phẩm \( S \) thì giá bán mỗi tạ sản phẩm \( S \) là \( P(x) = 6 - 0{,}0005x^2 \) (triệu đồng) với \( x \leq 40 \). Chi phí \( A \) phải bỏ ra cho \( x \) tạ sản phẩm \( S \) trong một tháng là \( C(x) = 10 + 3{,}5x \) (triệu đồng), và mỗi sản phẩm bán ra phải chịu thêm mức thuế là 1 triệu đồng. Hỏi trong một tháng \( B \) cần đặt hàng bao nhiêu tạ sản phẩm \( S \) thì \( A \) có được lợi nhuận lớn nhất, kết quả làm tròn đến hàng phần chục.
Câu 6: Trong không gian \( Oxyz \), cho hai điểm \( A(5;0;0) \), \( B(3;4;0) \) và điểm \( C \) nằm trên trục \( Oz \). Gọi \( H \) là trực tâm tam giác \( ABC \). Khi \( C \) di chuyển trên trục \( Oz \) thì \( H \) luôn thuộc một đường tròn cố định. Tính bán kính của đường tròn đó, kết quả làm tròn đến hàng phần trăm.