Đề thi thử tốt nghiệp THPT 2025 môn Toán -THPT Yên Lac - Vĩnh Phúc
Phần 1: Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Tổng số câu hỏi: 0
Câu 1: Cho $A$ và $B$ là hai biến cố độc lập, với $P(A) = 0{,}2024$, $P(B) = 0{,}2025$. Tính $P(A | B)$.
Câu 2: Phương trình $2\cos x - 1 = 0$ có một nghiệm là
Câu 3: Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm này là
Câu 4: Đạo hàm của hàm số $f(x) = \frac{1}{2}x^2 + \sin{x} - \sqrt{x}$ là:
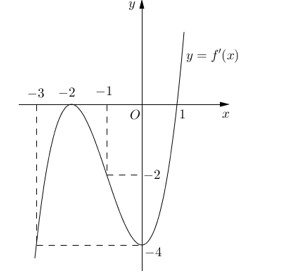
Câu 5: Cho hàm số $y = f(x)$ có đạo hàm trên $\mathbb{R}$ và hàm số $y = f'(x)$ là
hàm số bậc ba có đồ thị là đường cong như hình vẽ. Hàm số $y = f(x)$ đồng
biến trên khoảng nào sau đây?
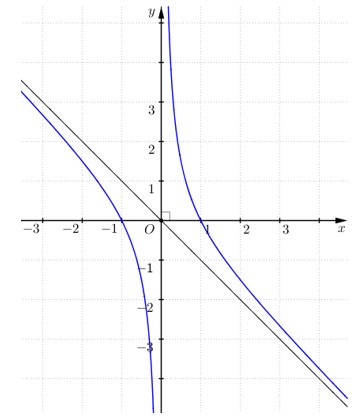
Câu 6: Đường cong trong hình là đồ thị của hàm số nào dưới đây?
Câu 7: Trong không gian $Oxyz$, cho hai điểm $A(3;-2;3)$ và $B(-1;2;5)$.
Tìm tọa độ trung điểm $I$ của đoạn thẳng $AB$.
Câu 8: Trong không gian $Oxyz$, cho điểm $M(2;1;3)$.
Gọi $A, B, C$ lần lượt là hình chiếu vuông góc của $M$ trên các trục tọa độ $Ox, Oy$ và $Oz$.
Phương trình mặt phẳng $(ABC)$ là
Câu 9: Trong không gian $Oxyz$, phương trình nào sau đây là phương trình chính tắc của đường thẳng?
Câu 10: Trong không gian $Oxyz$, cho mặt cầu có phương trình $(x - 1)^2 + (y + 3)^2 + z^2 = 9$.
Tọa độ tâm $I$ của mặt cầu đó là
Câu 11: Hàm số nào sau đây là một nguyên hàm của hàm số $y = \cot^2 x$?
Câu 12: Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$, $\int_{3}^{5} f(x) \,dx = 2$.
Biểu thức $\int_{5}^{3} f(x) \,dx$ bằng
Phần 2: Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Nếu cho một ý là đúng, thí sinh tích chọn, nếu cho 1 ý là sai, thí sinh bỏ trống.
Tổng số câu hỏi: 0
Câu 1: Cho hàm số $y = f(x) = \dfrac{x^2 + 3x}{x - 1}$.
Câu 2: Trong không gian $Oxyz$, cho các điểm $A(1;-3;5)$, $B(-3;7;1)$, $C(5;-1;17)$.
Câu 3: Một chất điểm $A$ xuất phát từ $O$, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật
\[ v_A(t) = \frac{1}{100}t^2 + \frac{13}{30} \quad (m/s), \]
trong đó $t$ (giây) là khoảng thời gian tính từ lúc $A$ bắt đầu chuyển động.
Từ trạng thái nghỉ, một chất điểm $B$ cũng xuất phát từ $O$, chuyển động thẳng cùng hướng với $A$ nhưng chậm hơn 10 giây so với $A$ và có gia tốc bằng $a$ $(m/s^2)$ ($a$ là hằng số). Sau khi $B$ xuất phát được 15 giây thì đuổi kịp $A$.
Câu 4: Khi kiểm tra sức khỏe tổng quát của bệnh nhân ở một bệnh viện, người ta được kết quả như sau:
Có 40% bệnh nhân đau dạ dày; có 30% bệnh nhân thường xuyên bị stress; trong số các bệnh nhân thường xuyên bị stress, có 80% bệnh nhân bị đau dạ dày. Chọn ngẫu nhiên một bệnh nhân.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
Tổng số câu hỏi: 0
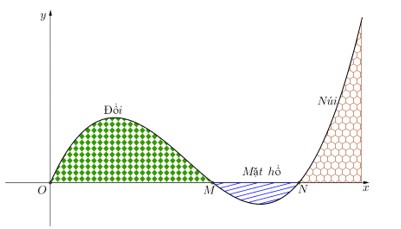
Câu 1: Lát cắt ngang của một vùng đất được mô hình hóa là một phần hàm số bậc ba \( y = f(x) \) có đồ thị như hình vẽ (đơn vị đo dài trên các trục là kilomet). Biết khoảng cách hai bên chân đồi \( OM = 2 \) (km), độ rộng của hồ nước \( MN = 1 \) (km) và ngọn đồi cao \( 528 \) (m). Độ sâu nhất của hồ nước là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét)?
Câu 2: Để chuẩn bị cho hoạt động cắm trại, bạn An tìm hiểu các mẫu lều cắm trại có dạng khối lăng trụ đứng ngũ giác với kích thước như trong hình a và hình b.
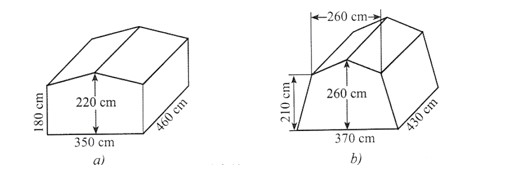
Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính V1 - V2, trong đó V1, V2 lần lượt là thể tích của mẫu lều cắm trại ở hình a, b. Giá trị của V1 - V2 bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?
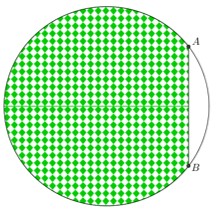
Câu 3: Ông A có miếng đất hình tròn có bán kính bằng \(5m\). Ông A tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn. Tuy nhiên, cần có một khoảng trống để dựng một cái chòi và để đồ dùng nên ông A bớt lại một phần đất nhỏ không trồng cây (phần màu trắng như hình vẽ), trong đó \(AB = 6m\). Gọi \(T\) là số tiền ông A nhận được sau khi thu hoạch (đơn vị nghìn đồng và làm tròn đến hàng đơn vị). Giá trị \(T\) bằng bao nhiêu?
Câu 4: Một phần thiết kế của một công trình đang xây dựng có dạng như hình bên, trong đó \(ABCD\) là hình vuông cạnh \(6m\), \(AM, BN, DP\) cùng vuông góc với \((ABCD)\), \(AM = 4m\), \(BN = 3m\), \(DP = 2m\). Góc giữa hai mặt phẳng \((ABCD)\) và \((MNP)\) (làm tròn kết quả đến hàng đơn vị của độ) là \(n^\circ\). Giá trị của \(n\) là bao nhiêu?
Câu 5: Trong không gian \( Oxyz \) (đơn vị đo dài trên các trục là kilomet), một trạm thu phát sóng điện thoại di động có đầu thu đặt tại điểm \( I(1;2;2) \) biết rằng bán kính phủ sóng của trạm là \(3 \, km\). Hai người sử dụng điện thoại lần lượt tại \( M(4;-4;2) \) và \( N(6;0;6) \). Gọi \( E(a,b,c) \) là một điểm thuộc ranh giới vùng phủ sóng của trạm sao cho tổng khoảng cách từ \( E \) đến vị trí \( M \) và \( N \) lớn nhất. Tính \( T = a + b + c \).
Câu 6: Hai bạn An, Bình cùng ném bóng rổ. Mỗi lần chỉ có một người ném với quy tắc như sau: Nếu ném trúng thì người đó sẽ ném tiếp, nếu ném trượt thì đến lượt người kia ném. Ở mỗi lần ném bóng, xác suất An ném trúng đều là \( 0.4 \) và xác suất Bình ném trúng đều là \( 0.6 \). Hai bạn rút thăm để quyết định người ném bóng đầu tiên. Xác suất người được ném đầu tiên là An và xác suất người được ném đầu tiên là Bình cùng bằng \( 0.5 \). Tìm xác suất để người ném bóng lần thứ 2 là Bình.