Đề thi thử tốt nghiệp THPT 2025 môn Toán -THPT Hai Bà Trưng - Vĩnh Phúc
Trắc nghiệm nhiều phương án lựa chọn
Tổng số câu hỏi: 0
Câu 1: Cho cấp số cộng $\left( u_{n} \right)$ với số hạng đầu $u_{1} = -6$ và công sai $d = 4$. Tính tổng $S$ của 14 số hạng đầu tiên của cấp số cộng đó.
Câu 2: Nghiệm của phương trình $\log_{16}(x+5) = \frac{1}{2}$ là:
Câu 3: Tung một đồng xu cân đối và đồng chất hai lần liên tiếp. Tính xác suất để hai lần tung đều xuất hiện mặt ngửa.
Câu 4. Một học sinh tô ngẫu nhiên $5$ câu trắc nghiệm. Xác suất để học sinh đó tô sai cả $5$ câu bằng:
Câu 5: Tiệm cận ngang của đồ thị hàm số $y = \frac{2x+1}{x-1}$ là
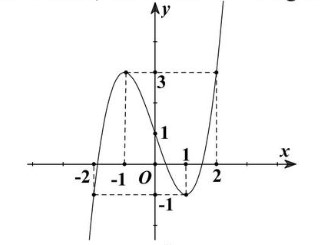
Câu 6. Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
Câu 7. Cho hàm số $f(x) = x^{2025} + 2024$. Khẳng định nào sau đây đúng?
Câu 8: Biết $\int_1^2 f(x)dx = 2$ và $\int_1^2 g(x)dx = 6$, khi đó $\int_1^2 [f(x) - g(x)]dx$ bằng
Câu 9: Một người công nhân của một nông trường thống kê lại đường kính thân gỗ của một số cây keo là trăm 7 năm tuổi được trồng ở một lâm trường ở bảng mẫu số liệu ghép nhóm sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm bằng
Câu 10. Khối lượng các túi đường được đóng gói (đơn vị là $kg$) được thống kê ở bảng sau.
Phương sai của mẫu số liệu ghép nhóm trên gần nhất với kết quả nào sau đây.
Câu 11. Trong không gian $Oxyz$, mặt phẳng $(\alpha)$ đi qua gốc tọa độ $O(0; 0; 0)$ và có vector pháp tuyến là $\vec{n} = (6; 3; -2)$ thì phương trình của $(\alpha)$ là
Câu 12. Trong không gian với hệ tọa độ $Oxyz$, trong các mặt cầu dưới đây, mặt cầu nào có bán kính $R = 2$?
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Nếu cho rằng một ý là đúng, thí sinh tích chọn đáp án đó.
Nếu cho rằng một ý là sai, thí sinh bỏ trống
Tổng số câu hỏi: 0
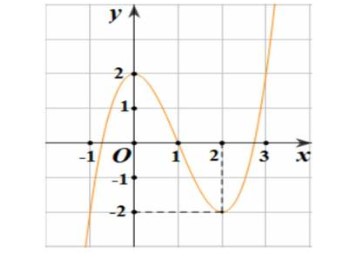
Câu 1. Cho hàm số $y = f(x) = x^3 - 3x^2 + 2$ có đồ thị như hình bên dưới
Câu 2. Cho parabol $(P): y = x^2$ và đường thẳng $d: y = 2x$
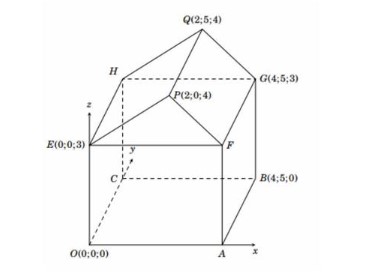
Câu 3. Hình minh họa sơ đồ một ngôi nhà trong hệ trục tọa độ $Oxyz$, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.
Câu 4. Trong không gian $Oxyz$ (đơn vị trên mỗi trục tính theo mét), một ngọn hải đăng được đặt ở vị trí $I(17; 20; 45)$. Biết rằng ngọn hải đăng đó được thiết kế với bán kính phủ sáng là $4 \text{ km}$.
Phần III. Câu hỏi trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 bằng cách điền kết quả vào ô trả lời.
Tổng số câu hỏi: 0
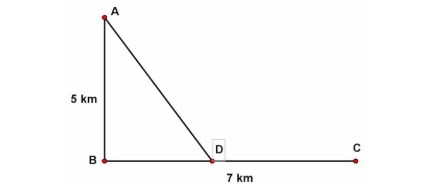
Câu 1. Một đoàn cứu trợ lũ lụt đang ở vị trí $A$ của một tỉnh miền trung muốn đến xã $C$ để tiếp tế lương thực và thuốc men. Để đi đến $C$, đoàn cứu trợ phải chèo thuyền từ $A$ đến vị trí $D$ với vận tốc $4(km/h)$, rồi đi bộ đến vị trí $C$ với vận tốc $6(km/h)$. Biết $A$ cách $B$ một khoảng $5km$, $B$ cách $C$ một khoảng $7km$ (hình vẽ). Gọi $D_0$ là vị trí để đoàn cứu trợ đi đến xã $C$ nhanh nhất. Tính $S = 100\sqrt{5.4D_0}$?
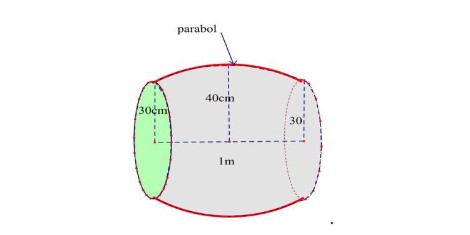
Câu 2. Một cái trống trường có bán kính các đáy là $30cm$, thiết diện vuông góc với trục và cách đều hai đáy có diện tích là $1600\pi (cm^2)$, chiều dài của trống là $1m$. Biết rằng mặt phẳng chứa trục cắt mặt xung quanh của trống là các đường Parabol. Gọi $V$ thể tích của cái trống. Tính $10V$?
Câu 3. Trường THPT A có $20\%$ học sinh tham gia câu lạc bộ âm nhạc, trong số học sinh đó có $85\%$ học sinh biết chơi đàn guitar. Ngoài ra, có $10\%$ số học sinh không tham gia câu lạc bộ âm nhạc cũng biết chơi đàn guitar. Chọn ngẫu nhiên 1 học sinh của trường. Giả sử học sinh đó biết chơi đàn guitar. Xác suất chọn được học sinh thuộc câu lạc bộ âm nhạc là bao nhiêu?
Câu 4. Một căn bệnh có $1\%$ dân số mắc phải. Một phương pháp chuẩn đoán được phát triển có tỷ lệ chính xác là $99\%$. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính $99\%$ số trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng $99$ trong $100$ trường hợp. Nếu một người kiểm tra và kết quả là dương tính (bị bệnh), xác suất để người đó thực sự bị bệnh là bao nhiêu?
Câu 5: Cho hình chóp $SABCD$, $ABCD$ là hình vuông cạnh $4$, $SA$ vuông góc với mặt phẳng đáy. Góc giữa $SC$ và $(ABCD)$ là $60^{\circ}$. Thể tích khối chóp $SABCD$ là $\frac{a}{3}\sqrt{b}$. Hãy tính giá trị của biểu thức $P = a + b$
Câu 6: Trong không gian $Oxyz$ cho tứ diện đều $ABCD$ có cạnh bằng $6$. Chọn hệ trục tọa độ $Oxyz$ như hình vẽ.
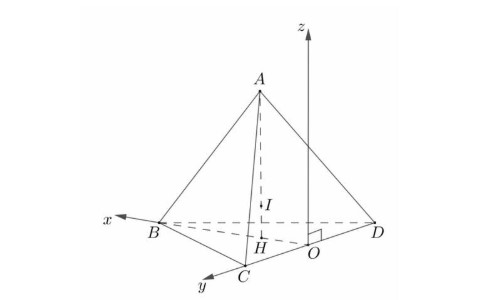Phương trình mặt cầu nội tiếp tứ diện có dạng $(x-a)^2 + (y-b)^2 + (z-c)^2 = R^2$. Hãy tính giá trị của biểu thức $P = a^2 + b^2 + c^2 + R^2$