Đề thi thử tốt nghiệp THPT 2025 môn Toán -THPT Chuyên Phan Bội Châu- Nghệ An
Phần I: Trắc nghiệm 4 phương án lựa chọn. Thí sinh chọn 1 đáp án đúng duy nhất
Tổng số câu hỏi: 0
Câu 1: Trong không gian với hệ tọa độ \( Oxyz \), cho hai vectơ \( \vec{a} = (1; -2; 1) \), \( \vec{b} = (-2; 1; 1) \). Tính góc giữa \( \vec{a} \) và \( \vec{b} \).
Câu 2: Trong không gian với hệ tọa độ \( Oxyz \), cho hai điểm \( A(1;2;3) \), \( B(3;8;5) \). Tọa độ trung điểm \( I \) của đoạn thẳng \( AB \) là
Câu 3: Đường tiệm cận xiên của đồ thị hàm số \[ y = \frac{x^2 + 2x - 3}{x - 2} \] là
Câu 4: Nghiệm của phương trình \( \sin x = \frac{1}{2} \) là
Câu 5: Cho hàm số \( y = f(x) \) xác định trên \( \mathbb{R} \) và có bảng biến thiên như sau:
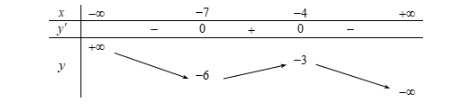
Điểm cực đại của hàm số \( y = f(x) \) là
Câu 6: Cho cấp số cộng (u_n) với u₁ = 2 và u₂ = 5. Tính u₄.
Câu 7: Cho $0 < a \neq 1, b > 0$. Biết $\log _{a}(b) = 3$ , tính $\log _{a}(ab) $.
Câu 8: Cho hàm số $y = f(x)$ xác định trên $\mathbb{R} \setminus \{-6\}$ và có bảng biến thiên như sau:
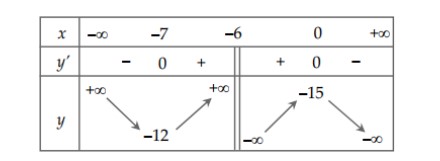Hàm số $y = f(x)$ đồng biến trên khoảng nào?
Câu 9: Cho hình tứ diện đều $ABCD$ có độ dài cạnh bằng $6$ cm. Gọi $M, N$ lần lượt là trung điểm cạnh $BC, CD$ và $G$ là trọng tâm tam giác $ABD$. Mặt phẳng $(GMN)$ cắt các cạnh $AB, AD$ tại $E, F$. Độ dài đoạn $EF$ bằng:
Câu 10: Đường tiệm cận đứng của đồ thị hàm số \( y = \frac{2x+3}{x-1} \) là:
Câu 11: Cho mẫu số liệu ghép nhóm có bảng tần số như sau:
Tính số trung bình của mẫu số liệu trên.
Câu 12: Cho hàm số \( y = \frac{ax + b}{x + c} \) có đồ thị như hình sau đây.
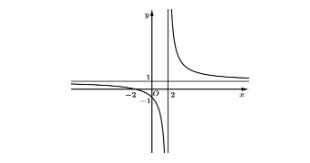Tính giá trị của biểu thức \( P = 2a - b + 3c \).
Phần 2: Trắc nghiệm chọn đúng sai.
Nếu cho một ý là đúng, thí sinh tích chọn đáp án.
Nếu cho một ý là sai, thí sinh không tích chọn.
Tổng số câu hỏi: 0
Câu 1: Cho hình chóp $S.ABCD$ có đáy là hình vuông và $SA$ vuông góc với đáy, $SA = 2a$, $AB = a$.
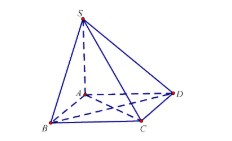
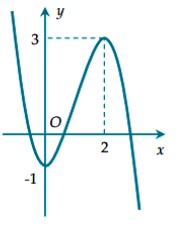
Câu 2: Cho hàm số \( f(x) = ax^3 + bx^2 + cx + d \) có đồ thị như hình sau đây:
Câu 3: Bạn An làm bài thi trắc nghiệm đúng sai gồm 4 câu hỏi mỗi câu 1 điểm, trong đó bạn làm chắc chắn đúng hai câu, còn hai câu còn lại bạn chọn ngẫu nhiên đúng hoặc sai.
Câu 4: Trong không gian với hệ trục \( Oxyz \) (đơn vị trên mỗi trục là 1 m), một flycam bay với vận tốc có độ lớn và hướng không đổi. Tại thời điểm \( t = 0 \), flycam ở vị trí \( A(1;2;3) \) và sau 10 phút nó ở vị trí \( B(21;32;33) \).
Phần 3. Trắc nghiệm trả lời ngắn. Thí sinh nhập kết quả vào ô trả lời
Tổng số câu hỏi: 0
Câu 1: Trong trung tâm thương mại Lotte thành phố Vinh, có một nhà hàng bán buffet hải sản. Khi nhà hàng bán với giá 200 ngàn đồng một suất thì mỗi ngày nhà hàng bán được 100 suất. Nhà hàng dự định có đợt giảm giá bán để kích cầu trong dịp cuối năm. Theo khảo sát từ thị trường thì mỗi lần giảm giá 10 ngàn đồng một suất thì nhà hàng bán thêm được 10 suất, hỏi nhà hàng cần bán với giá mới là bao nhiêu ngàn đồng một suất để doanh thu trong một ngày là lớn nhất?
Câu 2: Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân. Trong lực tác dụng lên chiếc máy có độ lớn là \(30N\) và được phân bố thành ba lực \(\overrightarrow{F_1}\), \(\overrightarrow{F_2}\), \(\overrightarrow{F_3}\) lên ba chân của giá đỡ.
Ba lực \(\overrightarrow{F_1}\), \(\overrightarrow{F_2}\), \(\overrightarrow{F_3}\) có độ lớn bằng nhau và góc tạo bởi mỗi chân của giá đỡ và mặt đất là \(60^\circ\).
Hỏi độ lớn của lực \(\overrightarrow{F_1}\) là bao nhiêu \(N\) (làm tròn đến hàng phần chục).
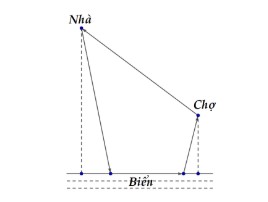
Câu 3: Nhà thầy Hùng cách bờ biển \(1km\). Mỗi buổi sáng thầy chạy bộ từ nhà ra bờ biển, sau đó chạy dọc bờ biển \(500m\), rồi thầy chạy qua chợ hải sản để lấy thức ăn trong ngày, cuối cùng thầy chạy về nhà.
Biết chợ hải sản cách bờ biển \(400m\) và cách nhà thầy Hùng \(1km\), tính quãng đường ngắn nhất mà thầy Hùng đã chạy trong mỗi buổi sáng (đơn vị \(m\) và làm tròn đến hàng đơn vị).
Câu 4: Hàm số \( y = \frac{x^2 - x + 1}{x - 1} \) có giá trị cực đại và giá trị cực tiểu lần lượt là \( a \) và \( b \).
Tính \( 3a + 2b \).
Câu 5: Thả một quả bóng từ độ cao \( 8m \), mỗi lần quả bóng sẽ nảy lên theo phương thẳng đứng đến độ cao bằng \( \frac{3}{4} \) độ cao trước đó.
Tính tổng quãng đường quả bóng đi chuyển kể từ lúc thả cho đến khi dừng lại (đơn vị là \( m \)).
Câu 6: Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \( A(1;2;3) \), \( B(7;10;6) \).
Hai điểm \( M, N \) thay đổi trên mặt phẳng \( (Oxy) \) sao cho \( MN = 4 \). Khi \( AM + BN \) nhỏ nhất, tính tổng hoành độ của \( M \) và tung độ của \( N \).