Đề thi thử học kỳ 1 môn Toán

Câu 1. Cho hai điểm A, B phân biệt và cố định, với I là trung điểm của AB. Tìm tập hợp các điểm thỏa mãn đẳng thức $\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|$.

A. Đường tròn tâm I, đường kính $\frac{{AB}}{2}$.

B. Đường tròn đường kính AB

C. Đường trung trực của đoạn thẳng AB

D. Đường trung trực của đoạn thẳng IA

Câu 2. Cho tam giác ABC, với M, N, P lần lượt là trung điểm của BC, CA, AB. Khẳng định nào sau đây sai?

A. $\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PM} = \overrightarrow 0$ .

B. $\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {MP}$ .

C. $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {AC} = \overrightarrow 0$ .

D. $\overrightarrow {AP} + \overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow 0$ .

Câu 3. TXĐ của hàm số $y = \sqrt {\frac{{3x + 5}}{{x - 1}} - 4}$ là với $\left( {a;b} \right]$ là các số thực. Tính tổng $a+b$?

A. a + b = - 8

B. a + b = 10

C. a + b = 8

D. a + b = 10

Câu 4. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu $x = y$ thì $t.x = t.y $

B. Nếu $x > y$ thì $x^3 > y^3$

C. Nếu số nguyên n có tổng các chữ số bằng 9 thì số tự nhiên n chia hết cho 3

D. Nếu $x > y$ thì $x^2 > y^2$

Câu 5. Cho tam giác ABC. Gọi M, N là các điểm thỏa mãn $\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 ,2\overrightarrow {NA} + 3\overrightarrow {NC} = \overrightarrow 0$ và $\overrightarrow {BC} = k\overrightarrow {BP}$. Tìm k để ba điểm M, N, P thẳng hàng.

A. $k = \frac{2}{3}$

B. $k = \frac{3}{5}$

C. $k = \frac{1}{3}$

D. $k = 3$

Câu 6. Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?

A. $\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB}$ .

B. $\overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {DC} - \overrightarrow {DA}$ .

C. $\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {CD}$ .

D. $\overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {OD} - \overrightarrow {OA}$ .

Câu 7. TXĐ của hàm số $y = \frac{1}{{\sqrt {2x - 5} }} + \sqrt {9 - x}$ là:

A. $D = \left( {\frac{5}{2};9} \right]$

B. $\left( {\frac{5}{2};9} \right)$

C. $\left[ {\frac{5}{2};9} \right)$

D. $D = \left[ {\frac{5}{2};9} \right]$

Câu 8. Cho tập $X = \left\{ {x \in N\left| {\left( {{x^2} - 4} \right)\left( {x - 1} \right)\left( {2{x^2} - 7x + 3} \right) = 0} \right.} \right\}$. Tính tổng S các phần tử của tập X.

A. S = $\frac{9}{2}$.

B. S = 5

C. S = 6

D. S = 4

Câu 9. Cho parabol (P) có phương trình $y = {x^2} - 2x + 4$. Tìm điểm mà parabol đi qua.

A. Q(4;2)

B. N(- 3;1)

C. P(4;0)

D. M(- 3; 19)

Câu 10. Cho hai điểm A và B phân biệt. Điều kiện cần và đủ để I là trung điểm AB là:

A. $\overrightarrow {IA} = \overrightarrow {IB}$ .

B. $\overrightarrow {IA} = -\overrightarrow {IB}$ .

C. $\overrightarrow {AI} = \overrightarrow {BI}$ .

D. $IA = IB$

Câu 11. Cho tập hợp $X = \left( { - \infty ;2} \right] \cap \left( { - 6; + \infty } \right)$. Khẳng định nào sau đây đúng?

A. $X = \left( { - 6;2} \right]$.

B. $X = \left( { - 6; + \infty } \right)$.

C. $X = \left( { - \infty ; + \infty } \right)$.

D. $X = \left( { - \infty ;2} \right]$.

Câu 12. Trong các câu sau, câu nào là mệnh đề?

A. Không được làm việc riêng trong giờ học!

B. Đi ngủ đi!

C. Trung Quốc là nước đông dân nhất thế giới.

D. Bạn học trường nào?

Câu 13. Cho 2 tập hợp $A = \left( { - 7;3} \right),B = \left( { - 4;5} \right)$. Chọn khẳng định đúng ?

A. $A \cup B = \left( { - 7; - 4} \right)$

B. $A{\rm{\backslash }}B = \left( { - 7; - 4} \right]$

C. $A{\rm{\backslash }}B = \left( { - 7; - 4} \right)$

D. $A \cap B = \left[ { - 4;3} \right)$

Câu 14. Chọn khẳng định đúng ?

A. Hàm số $y=f(x)$ được gọi là nghịch biến trên K nếu: $\forall {x_1};{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$

B. Hàm số $f(x)$ được gọi là đồng biến trên K nếu: $\forall {x_1};{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \le f\left( {{x_2}} \right)$

C. Hàm số $f(x)$ được gọi là đồng biến trên K nếu: $\forall {x_1};{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$

D. Hàm số $f(x)$ được gọi là đồng biến trên K nếu: $\forall {x_1};{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$

Câu 15. Tìm m để hàm số $y = {x^2} - 2x + 2m + 3$ có giá trị nhỏ nhất trên đoạn $[2;5]$ bằng $- 3$.

A. m = 0

B. m = - 9

C. m = 1

D. m = - 3

Câu 16. Cho hai tập hợp M, N thỏa mãn M \subset N. Mệnh đề nào sau đây đúng?

A. $M \cap N = N.$

B. $M\backslash N = N.$

C. $M \cap N = M.$

D. $M\backslash N = M.$

Câu 17. Trong các hàm số sau, hàm số nào là hàm số chẵn ?

A. $y = {x^2} + \frac{1}{x}$

B. $y = \frac{x}{{{x^4} - 2{x^2} + 1}}$

C. $y = \frac{1}{{4{x^3}}}$

D. $y = {\left( {2x - 1} \right)^{2018}} + {\left( {2x + 1} \right)^{2018}}$

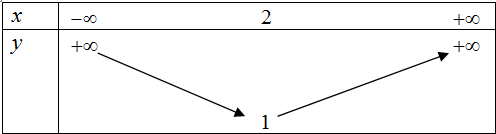
Câu 18. Tìm hàm số bậc hai có bảng biến thiên như hình vẽ dưới đây.

A. $y = {x^2} - 4x + 5$

B. $y = {x^2} - 4x - 5$

C. $y = - {x^2} + 4x - 3$

D. $y = {x^2} - 2x + 1$

Câu 19. Cho hình chữ nhật $ABCD$ và số thực $k > 0$. Tìm tập hợp các điểm M thỏa mãn đẳng thức $\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right| = k$.

A. Một đường thẳng.

B. Một đường tròn.

C. Một điểm.

D. Một đoạn thẳng.

Câu 20. Tìm tất cả các giá trị của b để hàm số $y = {x^2} + 2(b + 6)x + 4$ đồng biến trên khoảng $(6; + \infty )$.

A. $b \ge 0$

B. $b = - 12$

C. $b \ge - 12$

D. $b \ge - 9$

Câu 21. Tìm khoảng nghịch biến của hàm số $y = - {x^2} - 2x + 2017$.

A. $( - 1; + \infty )$

B. $( - 2; + \infty )$

C. $( - \infty ; - 1)$

D. $( - \infty ; 0)$

Câu 22. TXĐ của hàm số $y = \frac{{x + 2}}{{{{\left( {x - 3} \right)}^2}}}$ là:

A. $\left( { - \infty ;3} \right)$

B. $\left( {3; + \infty } \right)$

C. $R{\rm{\backslash }}\left\{ 3 \right\}$

D. $R$

Câu 23. Cho hai tập $A = \left[ { - 1;3} \right);\,B = \left[ {a;a + 3} \right]$. Với giá trị nào của a thì $A \cap B = \emptyset$.

A. $\left[ \begin{array}{l} a \ge 3\\ a < - 4 \end{array} \right.$

B. $\left[ \begin{array}{l} a > 3\\ a < - 4 \end{array} \right.$

C. $\left[ \begin{array}{l} a \ge 3\\ a \le - 4 \end{array} \right.$

D. $\left[ \begin{array}{l} a > 3\\ a \le - 4 \end{array} \right.$

Câu 24. Cho parabol (P) có phương trình $y = 3{x^2} - 2x + 4$. Trục đối xứng của parabol là đường thẳng:

A. $x = \frac{1}{3}$

B. $x = \frac{2}{3}$

C. $x = \frac{-2}{3}$

D. $x = \frac{-1}{3}$

Câu 25. Từ 10 điểm phân biệt, lập được tất cả bao nhiêu vecto khác vecto - không có điểm đầu, điểm cuối là 2 trong 10 điểm đã cho ?

A. 99

B. 90

C. 45

D. 100

Đề thi thử học kỳ 1 môn Toán - Lớp 10