Đề thi thử giữa học kỳ 1 môn Toán lớp 12 online - Mã đề 11

40 câu hỏi

45 phút

Toán

0 câu hỏi

45 phút

Toán

Câu 1:

Hỏi hàm số $y=2 x^{4}-5$ đồng biến trên khoảng nào?

A. $(0 ;+\infty)$

B. $\left(-\infty ;-\frac{1}{2}\right)$

C. $(-\infty ; 0)$

D. $\left(-\frac{1}{2} ;+\infty\right)$

Câu 2:

Số điểm cực trị của hàm số $y=-x^{3}+3 x^{2}+x+3$ là

A. 2

B. 3

C. 1

D. 0

Câu 3:

Tìm giá trị lớn nhất của hàm số $y=-x^{3}+3 x^{2}$ trên đoạn [-3;1]

A. $\max\limits _{[-3 ; 1]} y=2$

B. $\max\limits _{[-3 ; 1]} y=0$

C. $\max \limits _{[-3 ; 1]} y=54$

D. $\max\limits _{[-3 ; 1]} y=54$

Câu 4:

Đồ thị hàm số $y=\frac{2 x+3}{x+2}$ có các đường tiệm cận là:

A. $y=-2\text{ và }x=-2 .$

B. $y=2\text{ và }x=-2$

C. $y=-2\text{ và }x=2$

D. $y=2\text{ và }x=2$

Câu 5:

Cho đồ thị như hình vẽ bên. Đây là đồ thị của hàm số nào?

A. $y=x^{3}+3 x^{2}$

B. $y=-x^{3}+3 x^{2}+1$

C. $y=-x^{3}+2x^{2}$

D. $y=x^{3}-3 x^{2}-2$

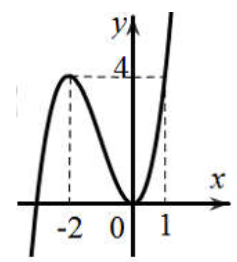
Câu 6:

Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp ba thì thể tích khối hộp tương ứng sẽ:

A. tăng 3 lần.

B. Tăng 6 lần.

C. Tăng 9 lần.

D. Tăng 27 lần.

Câu 7:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , $A B=3 a, A C=4 a$ , SB vuông góc (ABC), $S C= a\sqrt{41} $ . Tính thể tích khối chóp S.ABC theo a

A. $8 a^{3}$

B. $30 a^{3}$

C. $10 a^{3} \sqrt{2}$

D. $5 a^{3}$

Câu 8:

Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?

A. Hàm số f(x) đồng biến trên các khoảng $\begin{array}{l}(-\infty ; 1) \cup(1 ;+\infty)\end{array}$

B. Hàm số f(x) đồng biến trên $\mathbb{R}$

C. Hàm số f(x) đồng biến trên các khoảng $(-\infty ; 1) \text { và }(1 ;+\infty)$

D. Hàm số f(x) đồng biến trên các khoảng $(-\infty ; 2) \text { và }(2 ;+\infty)$

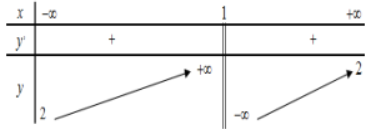
Câu 9:

Cho hàm số y =f(x) có bảng biến thiên như sau:

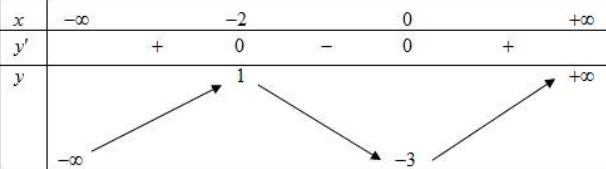
Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?

A. $(-2 ; 0)$

B. $(0 ;+\infty)$

C. $(-\infty ;-2)$

D. $(-3 ; 1)$

Câu 10:

Cho hàm số$y=f(x)$. Hàm số $y=f'(x)$ có đồ thị như hình vẽ

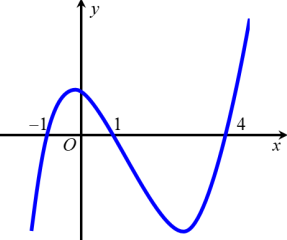
Hàm số $y=f\left(2-e^{x}\right)$ đồng biến trên khoảng:

A. $(0 ; \ln 3)$

B. $(2 ;+\infty)$

C. $(-\infty ; 1)$

D. $(1 ; 4)$

Câu 11:

Cho hàm số $y=x^{3}+17 x^{2}-24 x+8$. Kết luận nào sau đây là đúng?

A. $x_{C D}=1$

B. $x_{C D}=\frac{2}{3}$

C. $x_{C D}=-3$

D. $x_{C D}=-12$

Câu 12:

Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu?

A. $y=-10 x^{4}-5 x^{2}+7$

B. $y=-17 x^{3}+2 x^{2}+x+5$

C. $y=\frac{x-2}{x+1}$

D. $y=\frac{x^{2}+x+1}{x-1}$

Câu 13:

Cho hàm số y=f(x) có đạo hàm $f^{\prime}(x)=(x+1)(x-2)^{2}(x-3)^{3}(x+5)^{4}$ . Hỏi hàm số y =f(x) có mấy điểm cực trị?

A. 2

B. 3

C. 4

D. 5

Câu 14:

Cho hàm số y =f(x) . Hàm số y = f'(x) có đồ thị như hình vẽ:

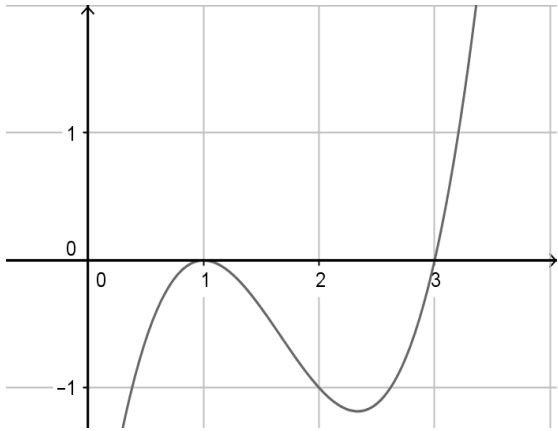
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số y=f(x) đạt cực đại tại x =1 .

B. Đồ thị hàm số y=f(x) có một điểm cực tiểu.

C. Hàm số y=f(x) đồng biến trên $(-\infty ; 1)$

D. Đồ thị hàm số y=f(x) có hai điểm cực trị

Câu 15:

Hàm số $y=x^{3}-3 x^{2}+m x-2$ đạt cực tiểu tại x = 2 khi?

A. $m>0$

B. $m \neq 0$

C. $m<0$

D. $m=0$

Câu 16:

Cho hàm số $y=(m-1) x^{3}-3 x^{2}-(m+1) x+3 m^{2}-m+2$ . Để hàm số có cực đại, cực tiểu thì:

A. $m=1$

B. $m \neq 1$

C. $m>1$

D. m tùy ý.

Câu 17:

Tìm tất cả các giá trị thực của m để hàm số $y=m x^{4}-(m+1) x^{2}+2 m-1$ có 3 điểm cực trị ?

A. $\left[\begin{array}{l}m<-1 \\ m>0\end{array}\right.$

B. $m<-1$

C. $-1<m<0$

D. $m>-1$

Câu 18:

Tìm tất cả các giá trị thực của tham số m để hàm số: $y=\frac{1}{3} x^{3}+m x^{2}+(m+6) x+m$ có cực đại và cực tiểu .

A. $-2<m<3$

B. $\left[\begin{array}{l}m<-2 \\ m>3\end{array} .\right.$

C. $\left[\begin{array}{l}m \leq-2 \\ m \geq 3\end{array}\right.$

D. $-2 \leq m \leq 3$

Câu 19:

Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{x^{3}}{3}+2 x^{2}+3 x-4$ trên [-4;0] lần lượt là M và m . Giá trị của M + m bằng

A. $\frac{4}{3}$

B. $-\frac{28}{3}$

C. $4$

D. $-\frac{4}{3}$

Câu 20:

Đồ thị hàm số sau có bao nhiêu đường tiệm cận $y=\frac{\sqrt{x-2}}{x^{2}-4 x+3} ?$

A. 4

B. 3

C. 2

D. 0

Câu 21:

hàm số phù hợp với bảng biến thiên sau. Phát biểu nào sau đây là đúng

A. Đồ thị hàm số có hai đường tiệm cận ngang là $y=-1 ; y=2$

B. Đồ thị hàm số có 2 đường tiệm cận đứng.

C. Đồ thị hàm số có đường tiệm cận đứng x = -1, tiệm cận ngang y = 2.

D. Đồ thị hàm số không có tiệm cận ngang.

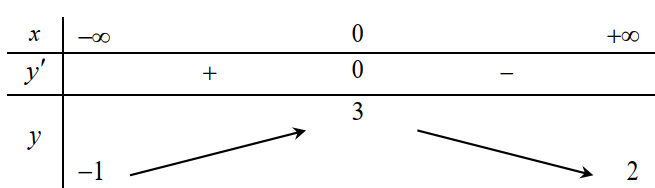
Câu 22:

Tìm phương trình tiệm cận đứng của đồ thị hàm số $y=\frac{x-1}{x+1}$

A. x=-1

B. y=1

C. y=-1

D. x=1

Câu 23:

Số mặt phẳng đối xứng của khối tứ diện đều là

A. 7

B. 8

C. 9

D. 6

Câu 24:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy và có độ dài bằng 2a . Thể tích khối tứ diện S.BCD là:

A. $\frac{a^{3}}{4}$

B. $\frac{a^{3}}{8}$

C. $\frac{a^{3}}{6}$

D. $\frac{a^{3}}{3}$

Câu 25:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Biết SA vuông góc với mặt phẳng đáy và $S A=a \sqrt{2}$. Tính thể tích khối chóp S.ABO.

A. $\frac{a^{3} \sqrt{2}}{3}$

B. $\frac{2 a^{3} \sqrt{2}}{12}$

C. $\frac{a^{3} \sqrt{2}}{12}$

D. $\frac{4 a^{3} \sqrt{2}}{3}$

Câu 26:

Cho hình chóp tam giác S.ABC với SA , SB , SC đôi một vuông góc và $S A=S B=S C=a$ . Tính thế tích của khối chóp S.ABC.

A. $\frac{1}{2} a^{3}$

B. $\frac{1}{6} a^{3}$

C. $\frac{2}{3} a^{3}$

D. $\frac{1}{3} a^{3}$

Câu 27:

Cho hình chóp S.ABCD đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy ABCD và mặt bên (SCD) hợp với đáy một góc 60⁰. Tính thể tích hình chóp S ABCD . .

A. $\frac{a^{3} \sqrt{3}}{3}$

B. $\frac{a^{3} \sqrt{3}}{6}$

C. $a^{3} \sqrt{3}$

D. $\frac{2 a^{3} \sqrt{3}}{3}$

Câu 28:

Với giá trị nào của thì đẳng thức $\sqrt[2016]{x^{2016}}=-x$ đúng

A. Không có giá trị nào

B. $x\ge 0$

C. x=0

D. $x\le 0$

Câu 29:

Căn bậc 4 của 3 là

A. $\sqrt[3]{4}$

B. $\sqrt[4]{3}$

C. $-\sqrt[4]{3}$

D. $\pm \sqrt[4]{3}$

Câu 30:

Với giá trị nào của thì biểu thức $\left(4-x^{2}\right)^{\frac{1}{3}}$ có nghĩa

A. $x \geq 2$

B. $-2<x<2$

C. $x \leq-2$

D. Không có giá trị x nào.

Câu 31:

So sánh hai số m và n nếu $3,2^{m}<3,2^{n}$ thì:

A. m>n

B. m=n

C. m<n

D. Không so sánh được.

Câu 32:

Cho $a=1+2^{-x}, b=1+2^{x}$ . Biểu thức biểu diễn b theo a là:

A. $\frac{a-2}{a-1}$

B. $\frac{a-1}{a}$

C. $\frac{a+2}{a-1}$

D. $\frac{a}{a-1}$

Câu 33:

Tập xác định của hàm số $y=\log _{0,5}(x+1)$ là:

A. $D=(-1 ;+\infty)$

B. $D=\mathbb{R} \backslash\{-1\}$

C. $D=(0 ;+\infty)$

D. $(-\infty ;-1)$

Câu 34:

Cho hàm số $y=3^{\frac{x}{2}}$có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với qua đường thẳng y=x

A. $y=\log _{\sqrt{3}} x$

B. $y=\log _{3} x^{2}$

C. $y=\log _{3}\left(\frac{x}{2}\right)$

D. $y=\frac{1}{2} \log _{3} x$

Câu 35:

Phương trình $3^{x^{3}-9 x+4}=81$ có mấy nghiệm?

A. 1

B. 2

C. 3

D. 4

Câu 36:

Cho phương trình $4.4^{x}-9.2^{x+1}+8=0$ . Gọi $x_1; x_2$ là hai nghiệm của phương trình trên. Khi đó, tích $x_1. x_2$ bằng:

A. -1

B. 2

C. -2

D. 1

Câu 37:

Tổng các nghiệm không âm của phương trình $\log _{\sqrt{3}} x-\log _{3}\left(2 x^{2}-4 x+3\right)=0$ là:

A. 1

B. 2

C. 4

D. 3

Câu 38:

Với giá trị m bằng bao nhiêu thì phương trình $\log _{2+\sqrt{3}}(m x+3)+\log _{2-\sqrt{3}}\left(m^{2}+1\right)=0$ có nghiệm là -1 ?

A. $\begin{aligned}&\left[\begin{array}{l}m=1 \\m=-1\end{array}\right.\end{aligned}$

B. $\left[\begin{array}{l}m=1 \\m=-2\end{array}\right.$

C. $m<3$

D. $m>3$

Câu 39:

Trong không gian Oxyz, cho $A(1 ; 0 ; 1), B(0;1;-1)$. Tính độ dài AB

A. $\sqrt 3$

B. $\sqrt 2$

C. 1

D. $2\sqrt 2$

Câu 40:

Tập nghiệm của phương trìnhlog $\log _{\sqrt{3}}|x-1|=2$ là:

A. $\{3\}$

B. $\{-3 ; 4\}$

C. $\{-2 ;-3\}$

D. $\{4 ;-2\}$

Câu hỏi

Hiển thị kết quả ngay sau khi trả lời

Trang 1/1