Hiển thị kết quả ngay sau khi trả lời

Đề thi thử giữa học kỳ 1 môn Toán lớp 12 online - Mã đề 06

Thí sinh đọc kỹ đề trước khi làm bài.

Tổng số câu hỏi: 0

Câu 1:

Đồ thị hàm số $y = {x^3} - 3{{\rm{x}}^2} + 2$ đi qua điểm nào?

A. $M\left( { - 1;4} \right)$

B. $N\left( {0; - 2} \right)$

C. $P\left( {1;0} \right)$

D. $Q\left( {2;2} \right)$

Câu 2:

Hình chóp tứ giác có mấy mặt?

A. 4

B. 8

C. 5

D. 6

Câu 3:

Cho hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ { - 1;3} \right]$ và có bảng biến thiên như hình bên dưới.

Mệnh đề nào sau đây là mệnh đề đúng?

A. Hàm số không có cực trị.

B. Hàm số đạt cực đại tại $x = 0$.

C. Hàm số đạt cực đại tại $x = 5$.

D. Hàm số đạt cực đại tại $x = 1$

Câu 4:

Thể tích V của khối chóp có diện tích đáy bằng B và chiều cao bằng h, được tính theo công thức

A. $V = \dfrac{1}{4}Bh$.

B. $V = \dfrac{1}{2}Bh$

C. $V = Bh$

D. $V = \dfrac{1}{3}Bh$

Câu 5:

Khối lăng trụ có diện tích đáy bằng 4, chiều cao bằng 3 có thể tích bằng

A. 12

B. 6

C. 4

D. 8

Câu 6:

Đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{x + 1}}{{x - 2}}$ có phương trình là

A. $y = 2$

B. $x = 1$

C. $x = 2$

D. $y = 1$

Câu 7:

Đường tiệm cận ngang của đồ thị hàm số $y = \dfrac{{x + 1}}{{x - 2}}$ có phương trình là

A. $y = 2$

B. $x = 1$

C. $x = 2$

D. $y = 1$

Câu 8:

Khối lập phương cạnh bằng 2 có thể tích bằng

A. 4

B. 2

C. 8

D. 16

Câu 9:

Hàm số $y = \dfrac{{3 - 2x}}{{x + 7}}$ nghịch biến trên khoảng nào sau đây?

A. $\left( { - \infty ;\dfrac{3}{2}} \right)$

B. $\left( { - \infty ; + \infty } \right)$

C. $\left( { - \infty ; - 7} \right)$

D. $\left( { - 8; + \infty } \right)$

Câu 10:

Hàm số ${x^4} + 2{x^2} - 3$ có bao nhiêu điểm cực trị?

A. 1

B. 3

C. 0

D. 2

Câu 11:

Cho hàm số $y = f\left( x \right) = {x^2} - 2x + 3$. Mệnh đề nào sau đây đúng?

A. $\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 3$

B. $\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 2$

C. $\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 6$

D. $\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = 0$

Câu 12:

Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào?

A. $y = {x^4} + 2{x^2} - 3$

B. $y = {x^4} - 2{x^2} - 3$

C. $y = - {x^4} - 2{x^2} + 3$

D. $y = - {x^4} + 2{x^2} + 3$

Câu 13:

Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?

A. $y = \dfrac{{x - 1}}{{x + 1}}$

B. $y = \dfrac{{x + 1}}{{x - 1}}$

C. $y = \dfrac{{2x - 3}}{{2x - 2}}$

D. $y = \dfrac{x}{{x - 1}}$

Câu 14:

Số tiếp tuyến của đồ thị hàm số $y = {x^4} - 2{x^2} - 3$ song song với trục hoành là :

A. một

B. ba

C. hai

D. không

Câu 15:

Cho hàm số $f\left( x \right)$ có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $\left( { - 2;{\mkern 1mu} {\mkern 1mu} 0} \right)$

B. $\left( {2; + \infty } \right)$

C. $\left( {0;{\mkern 1mu} {\mkern 1mu} 2} \right)$

D. $\left( {0; + \infty } \right)$

Câu 16:

Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ

Hàm số đồng biến trên khoảng:

A. $\left( { - 2; - 1} \right)$

B. $\left( { - 1;0} \right)$

C. $\left( {0;2} \right)$

D. $\left( { - 2;0} \right)$

Câu 17:

Tổng số mặt, số cạnh và số đỉnh của một hình lập phương là:

A. 26

B. 24

C. 30

D. 22

Câu 18:

Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là một hình thoi cạnh a, $\widehat {ABC} = {120^0}$; $AA' = 4a$ Tính khoảng cách giữa hai đường thẳng A’C và BB’?

A. $\dfrac{{a\sqrt 3 }}{2}$

B. $a\sqrt 3 $

C. $\dfrac{a}{2}$

D. $\dfrac{a}{{\sqrt 3 }}$

Câu 19:

Đồ thị hàm số $y = \dfrac{{2x - 3}}{{x - 1}}$ có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

A. $x = 1$ và $y = 2$

B. $x = 2$ và $y = 1$

C. $x = 1$ và $y = {\rm{\;}} - 3$

D. $x = {\rm{\;}} - 1$ và $y = 2$

Câu 20:

Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {2 - x} \right)\left( {x + 3} \right).$ Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên các khoảng $\left( { - \infty ;3} \right),\left( {2; + \infty } \right).$

B. Hàm số nghịch biến trên khoảng $\left( { - 3;2} \right).$

C. Hàm số nghịc biến trên các khoảng $\left( { - 3; - 1} \right),\left( {2; + \infty } \right).$

D. Hàm số đồng biến trên khoảng $\left( { - 3;2} \right).$

Câu 21:

Có bao nhiêu điểm thuộc đồ thị hàm số $y = \dfrac{{2x - 1}}{{x - 1}}$ thỏa mãn tiếp tuyến với đồ thị tại điểm đó có hệ số góc bằng 2018?

A. 1

B. 0

C. Vô số

D. 2

Câu 22:

Số giao điểm của đồ thị hàm số $y = {x^4} - 2{x^2} + 1$ và đường thẳng $y = 1$ là:

A. $1$

B. $2$

C. $3$

D. $4$

Câu 23:

Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết $SB = a$ và SC hợp với (SAB) một góc 300 và (SAC) hợp với (ABC) một góc 600. Thể tích khối chóp là:

A. $\dfrac{{{a^3}\sqrt 3 }}{{27}}$

B. $\dfrac{{{a^3}\sqrt 3 }}{9}$

C. $\dfrac{{{a^3}}}{{27}}$

D. $\dfrac{{{a^3}}}{9}$

Câu 24:

Số đường tiệm cận của đồ thị hàm số $y = \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}}$ là:

A. 2

B. 0

C. 1

D. 3

Câu 25:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, ABB'A', ADD'A' lần lượt bằng $36c{m^2}$, $225c{m^2}$, $100c{m^2}$. Tính thể tích khối A.A'B'D'.

A. $900c{m^3}.$

B. $150c{m^3}.$

C. $250c{m^3}.$

D. $300c{m^3}.$

Câu 26:

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ

Đồ thị hàm số $y = \left| {f\left( x \right) - 2m} \right|$ có 5 điểm cực trị khi và chỉ khi

A. $m \in \left( {4;11} \right)$.

B. $m \in \left[ {2;\dfrac{{11}}{2}} \right]$.

C. $m \in \left( {2;\dfrac{{11}}{2}} \right)$.

D. $m = 3$.

Câu 27:

Một đường thẳng cắt đồ thị hàm số $y = {x^4} - 2{x^2}$ tại 4 điểm phân biệt có hoành độ $0,{\mkern 1mu} 1,{\mkern 1mu} m$ và n. Tính $S = {m^2} + {n^2}.$

A. $S = 1.$

B. $S = 2.$

C. $S = 0.$

D. $S = 3.$

Câu 28:

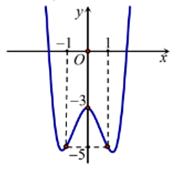
Đồ thị sau đây là của hàm số $y = {x^4} - 3{x^2} - 3.$ Với giá trị nào của m thì phương trình ${x^4} - 3{x^2} - 3 = m$ có đúng 3 nghiệm phân biệt.

A. $m = {\rm{\;}} - 4$

B. $m = {\rm{\;}} - 3$

C. $m = 0$

D. $m = {\rm{ \;}} - 5$

Câu 29:

Cho khối chóp S.ABC có $SA \bot \left( {ABC} \right)$, $SA = a$, $AB = a$, $AC = 2a$, $BC = a\sqrt 3 .$ Tính thể tích khối chóp S.ABC.

A. ${a^3}\sqrt 3 .$

B. $\dfrac{{{a^3}\sqrt 3 }}{6}.$

C. $\dfrac{{{a^3}\sqrt 3 }}{2}.$

D. $\dfrac{{{a^3}\sqrt 3 }}{3}.$

Câu 30:

Đồ thị hàm số $y = \dfrac{x}{{\sqrt {{x^2} - 1} }}$ có bao nhiêu đường tiệm cận

A. $4$.

B. $3$.

C. $1$.

D. $2$.

Câu 31:

Xét các khẳng định sau

i) Nếu hàm số $y = f\left( x \right)$ có đạo hàm cấp hai trên $\mathbb{R}$và đạt cực tiểu tại $x = {x_0}$ thì $\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) > 0}\end{array}} \right.$

ii) Nếu hàm số $y = f\left( x \right)$ có đạo hàm cấp hai trên $\mathbb{R}$và đạt cực đại tại $x = {x_0}$ thì $\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) < 0}\end{array}} \right.$

iii) Nếu hàm số $y = f\left( x \right)$ có đạo hàm cấp hai trên $\mathbb{R}$ và $f''({x_0}) = 0$thì hàm số không đạt cực trị tại $x = {x_0}$

Số khẳng định đúng trong các khẳng định trên là

A. 0

B. 1

C. 2

D. 3

Câu 32:

Gọi I là tâm đối xứng của đồ thị hàm số $y = \dfrac{{2x - 3}}{{x + 2}}$. Tìm tọa độ điểm $I$.

A. $I\left( { - 2;2} \right)$

B. $I\left( { - 2;1} \right)$

C. $I\left( {1;2} \right)$

D. $I\left( { - 2; - \dfrac{3}{2}} \right)$.

Câu 33:

Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng BC' và B'D' là:

A. ${45^0}$.

B. ${30^0}$.

C. ${60^0}$.

D. ${90^0}$.

Câu 34:

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right) = 2{x^3} + 3{x^2} - 1$ trên đoạn$\left[ { - 2; - \dfrac{1}{2}} \right]$. Tính $P = M - m$.

A. $P = {\rm{\;}} - 5$

B. $P = 1$

C. $P = 5$

D. $P = 4$

Câu 35:

Khối đa diện đều loại $\left\{ {5;3} \right\}$ có bao nhiêu mặt?

A. 12 mặt

B. 6 mặt

C. 10 mặt

D. 8 mặt

Câu 36:

Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'\left( x \right) = {\rm{\;}} - \left( {x - 10} \right){\left( {x - 11} \right)^2}{\left( {x - 12} \right)^{2019}}$ . Khẳng định nào dưới đây đúng ?

A. Hàm số đồng biến trên các khoảng $\left( {10;11} \right)$ và $\left( {12; + \infty } \right)$

B. Hàm số có ba điểm cực trị

C. Hàm số đồng biến trên khoảng $\left( {10;12} \right)$

D. Hàm số đạt cực đại tại $x = 2$ và đạt cực tiểu tại $x = 1$ và $x = 3.$

Câu 37:

Cho hình chóp S.ABCD có đáy là hình thoi cạnh $a$, $\angle BAD = {60^0}$, cạnh bên $SA = a$ và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ $B$ đến mặt phẳng $\left( {SCD} \right)$.

A. $\dfrac{{a\sqrt {21} }}{7}$

B. $\dfrac{{a\sqrt {15} }}{7}$

C. $\dfrac{{a\sqrt {21} }}{3}$

D. $\dfrac{{a\sqrt {15} }}{3}$

Câu 38:

Cho hàm số $y = \dfrac{{x + 3}}{{ - 1 - x}}$. Tìm mệnh đề đúng trong các mệnh đề sau:

A. Hàm số nghịch biến trên các khoảng $\left( { - \infty ; - 1} \right)$ và $\left( { - 1; + \infty } \right)$.

B. Hàm số đồng biến trên các khoảng $\left( { - \infty ;1} \right)$ và $\left( {1; + \infty } \right)$.

C. Hàm số đồng biến trên $\mathbb{R}\backslash \left\{ 1 \right\}$.

D. Hàm số đồng biến trên $\left( {2; + \infty } \right)$.

Câu 39:

Tìm giá trị nhỏ nhất của hàm số $y = \dfrac{{{x^2} - 5}}{{x + 3}}$ trên $\left[ {0;2} \right].$

A. $\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = \dfrac{{ - 5}}{3}$

B. $\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = \dfrac{{ - 1}}{3}$

C. $\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = - 2$

D. $\mathop {\min }\limits_{x \in \left[ {0;2} \right]} {\mkern 1mu} y = - 10$

Câu 40:

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy, $AB = 2a,{\mkern 1mu} {\mkern 1mu} \widehat {BAC} = {60^0}$ và $SA = a\sqrt 2 .$ Góc giữa đường thẳng SB và mặt phẳng $\left( {SAC} \right)$ bằng

A. ${30^0}.$

B. ${45^0}.$

C. ${60^0}.$

D. ${90^0}.$