Thi thử trắc nghiệm môn Lý thuyết điều khiển tự động online

Câu 1:

Hệ thống bất biến theo thời gian là hệ thống có:

A. Tín hiệu ra không thay đổi theo thời gian

B. Phương trình vi phân mô tả hệ thống không thay đổi

C. Tín hiệu vào không thay đổi theo thời gian

D. Hệ số của phương trình vi phân mô tả hệ thống không thay đổi

Câu 2:

Tìm nghiệm của hệ thống có phương trình đặc tính sau: s²+ 4s + 3 = 0

A. s1= -0.268; s2= -3.732

B. s1= -0.586; s2= -3.414

C. s1= -1; s2= -3

D. s1= -2; s2= -2

Câu 3:

Hệ thống có quỹ đạo nghiệm số như hình vẽ. Số nghiệm cực của hệ thống là:

A. 2

B. 3

C. 4

D. 5

Câu 4:

Biểu đồ Bode biên độ của khâu tích phân lý tưởng G(s)=1/s

A. đi qua điểm ω =0 và có độ dốc là 20dB/dec

B. đi qua điểm ω =0 và có độ dốc là -20dB/dec

C. đi qua điểm ω =1 và có độ dốc là 20dB/dec

D. đi qua điểm ω =1và có độ dốc là -20dB/dec

Câu 5:

Hệ SISO là hệ thống có:

A. Nhiều ngõ vào- nhiều ngõ ra

B. Nhiều ngõ vào - một ngõ ra

C. Một ngõ vào – một ngõ ra

D. Một ngõ vào – nhiều ngõ ra

Câu 6:

Số lần đổi dấu của số hạng ở cột 1 bảng Routh bằng số nghiệm:

A. Có phần thực âm

B. Có phần thực dương

C. Nghiệm phức của phương trình

D. Có phần thực bằng 0

Câu 7:

Hàm truyền đạt của hệ thống nối tiếp:

A. G(s)= Tổng của các Gi(s)

B. G(s) = Tích của các Gi(s)

C. G(s)= Hiệu của các Gi(s)

D. Tỉ số giữa tín hiệu ra và tín hiệu vào

Câu 8:

DAC là:

A. Bộ chuyển đổi tín hiệu từ dạng số sang dạng tương tự

B. Bộ khuếch đại tín hiệu

C. Bộ chuyển đổi tín hiệu từ dạng tương tự sang dạng số

D. Bộ thay đổi tần số của tín hiệu vào

Câu 9:

Hàm truyền của hệ thống:

A. Là tỉ số giữa tín hiệu ra và tín hiệu vào

B. Là tỉ số giữa biến đổi Laplace của tín hiệu ra và biến đổi Laplace của tín hiệu vào khi điều kiện đầu bằng 0

C. Phụ thuộc vào tín hiệu ra và tín hiệu vào

D. Mô tả chức năng của các phần tử và sự tác động qua lại giữa chúng trong hệ

Câu 10:

Hệ thống rời rạc là ổn định nếu tất cả các nghiệm của phương trình đặc tính:

A. Nằm bên trái mặt phẳng phức

B. Nằm bên trong vòng tròn đơn vị

C. Nằm bên ngoài vòng tròn đơn vị

D. Nằm bên phải mặt phẳng phức

Câu 11:

Hàm truyền đạt $G(s) = \frac{{{V_o}(s)}}{{{V_i}(s)}}{\cos ^{ - 1}}\theta $ của mạch điện ở hình sau là:

A. $- \frac{{{R_2}}}{{{R_1}}} - \frac{1}{{{R_1}Cs}}$

B. $- \frac{{{R_2}}}{{{R_1}}} + \frac{1}{{{R_1}Cs}}$

C. $\frac{{{R_2}}}{{{R_1}}} + \frac{1}{{{R_1}Cs}}$

D. $ - \frac{{{R_1}}}{{{R_2}}} - \frac{1}{{{R_1}Cs}}$

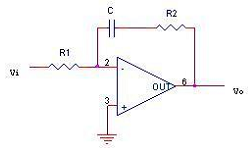
Câu 12:

Đặc điểm của khâu hiệu chỉnh PD (Proportional Derivative) là:

A. Làm chậm đáp ứng của hệ thống, tăng thời gian quá độ

B. Làm chậm đáp ứng của hệ thống, giảm thời gian quá độ

C. Làm nhanh đáp ứng của hệ thống, giảm thời gian quá độ

D. Làm nhanh đáp ứng của hệ thống, tăng thời gian quá độ

Câu 13:

Tiêu chuẩn IAE (Integral of the Absolute magnitude of the Error - tích phân trị tuyệt đối biên độ sai số ):

A. ${J_1} = \int\limits_{ - \infty }^{ + \infty } {|e(t)|dt}$

B. ${J_1} = \int\limits_0^{ + 1} {|e(t)|dt} $

C. ${J_1} = \int\limits_0^{ + \infty } {|e(t)|dt}$

D. ${J_1} = \int\limits_{ - \infty }^{ + \infty } {|e(t)|dt} $

Câu 14:

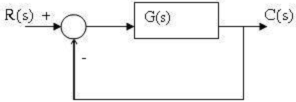
Cho hệ thống hồi tiếp âm đơn vị sau. Sai số xác lập e_xl là:

A. ${e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)}}$

B. ${e_{xl}} = \mathop {\lim }\limits_{t \to 0} e(t) = \mathop {\lim }\limits_{s \to \infty } \frac{{sR(s)}}{{1 + G(s)}}$

C. ${e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{R(s)}}{{1 + G(s)}}$

D. ${e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sG(s)}}{{1 + R(s)}}$

Câu 15:

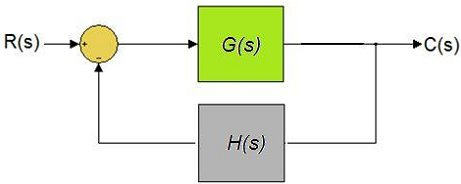
Cho hệ thống hồi tiếp âm đơn vị sau. Sai số xác lập e_xl là:

A. ${e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)H(s)}}$

B. ${e_{xl}} = \mathop {\lim }\limits_{t \to 0} e(t) = \mathop {\lim }\limits_{s \to \infty } \frac{{sR(s)}}{{1 + G(s)H(s)}}$

C. ${e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{R(s)}}{{1 + G(s)}}$

D. ${e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sG(s)}}{{1 + R(s)G(s)}}$

Câu 16:

Xác định hàm truyền tương đương của hệ thống nối tiếp như hình vẽ:

A. ${G_{td}}(s) = \frac{1}{{{s^2} + 5s + 2}}$

B. ${G_{td}}(s) = \frac{{s + 2}}{{{s^2} + 5s + 6}}$

C. ${G_{td}}(s) = \frac{1}{{{s^2} + 3s + 6}}$

D. ${G_{td}}(s) = \frac{1}{{{s^2} + 5s + 6}}$

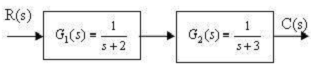
Câu 17:

Hàm truyền tương đương của hệ thống hồi tiếp như hình vẽ là:

A. ${G_{td}}(s) = \frac{{s + 3}}{{{s^2} + 5s + 7}}$

B. ${G_{td}}(s) = \frac{{s + 2}}{{{s^2} + 5s + 7}}$

C. ${G_{td}}(s) = \frac{1}{{{s^2} + 5s + 2}}$

D. ${G_{td}}(s) = \frac{{s + 2}}{{{s^2} + 5s + 6}}$

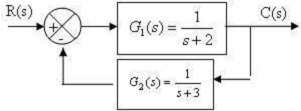
Câu 18:

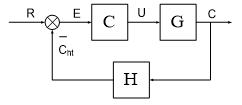
Cho hệ thống có cấu trúc sau:

Tìm hàm truyền tương đương của hệ thống:$H(s) = 1$$G(s) = \frac{{s + 3}}{{{s^2} + 3s + 1}}$$C(s) = \frac{3}{{5s + 1}}$

A. ${G_{td}}(s) = \frac{{3s + 10}}{{5{s^3} + 16{s^2} + 11s + 10}}$

B. ${G_{td}}(s) = \frac{{3s + 9}}{{5{s^3} + 16{s^2} + 11s + 11}}$

C. ${G_{td}}(s) = \frac{{3s + 9}}{{5{s^3} + 16{s^2} + 11s + 10}}$

D. ${G_{td}}(s) = \frac{{s + 9}}{{5{s^3} + 16{s^2} + 11s + 10}}$

Câu 19:

Cho hệ thống có hàm truyền tương đương sau: ${G_{td}}(s) = \frac{{s + 1}}{{{s^3} + 3{s^2} + 4s + 1}}$

A. Hệ thống không ổn định, có 3 nghiệm cực bên phải mặt phẳng phức

B. Hệ thống ổn định, có 3 nghiệm cực nằm bên trái mặt phẳng phức

C. Hệ thống không ổn định, có 2 nghiệm cực bên phải mặt phẳng phức, 1 nghiệm cực bên trái mặt phẳng phức

D. Hệ thống không ổn định, có 1 nghiệm cực bên phải mặt phẳng phức, 2 nghiệm cực bên trái mặt phẳng phức

Câu 20:

Cho hệ thống có hàm truyền tương đương sau:

${G_{td}}(s) = \frac{{s + 1}}{{{s^3} - {s^2} + 4s + 1}}$

Xét tính ổn định của hệ thống trên:

A. Hệ thống ổn định, có 2 nghiệm cực bên phải mặt phẳng phức

B. Hệ thống ổn định, có 2 nghiệm cực nằm bên trái mặt phẳng phức

C. Hệ thống không ổn định, có 2 nghiệm cực bên phải mặt phẳng phức, 1 nghiệm cực bên trái mặt phẳng phức

D. Hệ thống không ổn định, có 1 nghiệm bên phải mặt phẳng phức, 2 nghiệm cực bên trái mặt phẳng phức

Câu 21:

Cho hệ thống có hàm truyền tương đương sau:

${G_{td}}(s) = \frac{{s + 1}}{{{s^3} + 3{s^2} + 4s}}$Xét tính ổn định của hệ thống trên:

A. Hệ thống không ổn định, có 3 nghiệm cực bên phải mặt phẳng phức

B. Hệ thống ổn định, có 2 nghiệm cực nằm bên trái mặt phẳng phức

C. Hệ thống không ổn định, có 2 nghiệm cực bên phải mặt phẳng phức, 1 nghiệm cực bên trái mặt phẳng phức

D. Hệ thống ở biên giới ổn định, có 1 nghiệm cực nằm trên trục ảo, 2 nghiệm cực bên trái mặt phẳng phức

Câu 22:

Cho hệ thống có hàm truyền tương đương sau:

${G_{td}}(s) = \frac{{s + 1}}{{{s^3} + 3{s^2} - s + 1}}$

Xét tính ổn định của hệ thống trên:

A. Hệ thống ổn định, có 3 nghiệm cực bên trái mặt phẳng phức

B. Hệ thống ổn định, có 2 nghiệm cực nằm bên trái mặt phẳng phức

C. Hệ thống không ổn định, có 2 nghiệm cực bên phải mặt phẳng phức, 1 nghiệm cực bên trái mặt phẳng phức

D. Hệ thống ở biên giới ổn định

Câu 23:

Cho hệ thống có hàm truyền tương đương sau:

Xét tính ổn định của hệ thống trên:${G_{td}}(s) = \frac{{s + 1}}{{{s^3} + {s^2} + 4s + 1}}$

A. Hệ thống ổn định, có 3 nghiệm cực bên trái mặt phẳng phức

B. Hệ thống không ổn định, có 2 nghiệm cực nằm bên trái mặt phẳng phức

C. Hệ thống không ổn định, có 2 nghiệm cực bên phải mặt phẳng phức, 1 nghiệm cực bên trái mặt phẳng phức

D. Hệ thống không ổn định, có 1 nghiệm cực bên phải mặt phẳng phức, 2 nghiệm cực bên trái mặt phẳng phức

Câu 24:

Cho hàm truyền $G(s) = \frac{{20}}{{{s^2} + 4s + 8}}$ , hãy lập phương trình trạng thái.

A. $A = \left[ {\begin{array}{*{20}{c}}0&1\\{ - 3}&{ - 8}\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}20\\0\end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}}1&0\end{array}} \right]$

B. $A = \left[ {\begin{array}{*{20}{c}}0&1\\{ - 2}&{ - 1}\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}0\\20\end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}}1&0\end{array}} \right]$

C. $A = \left[ {\begin{array}{*{20}{c}}0&1\\{ - 8}&{ - 4}\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}0\\20\end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}}1&0\end{array}} \right]$

D. $A = \left[ {\begin{array}{*{20}{c}}1&1\\{ - 2}&{ - 8}\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}20\\0\end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}}1&0\end{array}} \right]$

Câu 25:

Cho hàm truyền $G(s) = \frac{2}{{{s^2} + 2s + 8}}$ , hãy lập phương trình trạng thái

A. $A = \left[ {\begin{array}{*{20}{c}}0&1\\{ - 8}&{ - 2}\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}0\\2\end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}}1&0\end{array}} \right]$

C. $A = \left[ {\begin{array}{*{20}{c}}0&1\\{ - 8}&{ - 2}\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}0\\20\end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}}1&0\end{array}} \right]$

Thi thử trắc nghiệm môn Lý thuyết điều khiển tự động online - Đề #2